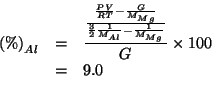(
A ![]() di una soluzione
di una soluzione ![]() di acido formico (
di acido formico (![]() )
vengono aggiunti
)
vengono aggiunti ![]() di formiato di potassio
(
di formiato di potassio
(![]() ). Calcolare il
). Calcolare il ![]() della soluzione risultante assumendo
che la variazione di volume in seguito all'aggiunta del solido sia
trascurabile.
della soluzione risultante assumendo
che la variazione di volume in seguito all'aggiunta del solido sia
trascurabile.
(
![]() )
)
Dati:
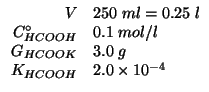
Altri simboli:
| massa molare di |
|
| numero di moli di |
Dopo l'aggiunta del sale alla soluzione dell'acido, ci si trova in
presenza di una soluzione tampone, che puo' essere trattata nel modo
usuale, trascurando l'autoionizzazione dell'acqua.

Le concentrazioni di equilibrio devono soddisfare la legge dell'azione
di massa:
Dato il valore di ![]() e la presenza dell'anione
dell'acido, si puo' assumere in prima
approssimazione che la reazione sia poco spostata verso destra: cio'
consente di trascurare
e la presenza dell'anione
dell'acido, si puo' assumere in prima
approssimazione che la reazione sia poco spostata verso destra: cio'
consente di trascurare
![]() come addendo. Si ottiene
cosi':
come addendo. Si ottiene
cosi':
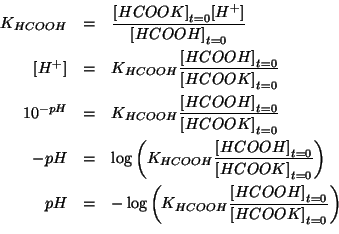
![]() coincide con la concentrazione data, mentre
coincide con la concentrazione data, mentre
![]() si ricava facilmente note la massa e la
massa molare di
si ricava facilmente note la massa e la
massa molare di ![]() e il volume della soluzione:
e il volume della soluzione:
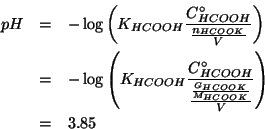
Alla luce del valore ottenuto, possiamo senz'altro affermare che
l'autoionizzazione dell'acqua poteva effettivamente essere
trascurata. Inoltre, per quanto riguarda il valore di
![]() in rapporto a quello di
in rapporto a quello di
![]() e
e
![]() , si ha:
, si ha:
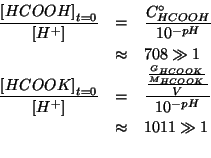
Una possibile reazione per convertire il metanolo in etanolo e' la seguente:
Utilizzando i seguenti dati termodinamici a ![]() :
:
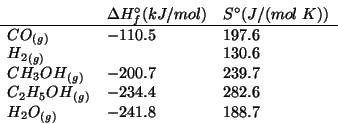
Dati:

Altri simboli:
| costante dei gas:
|
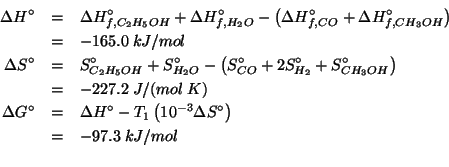
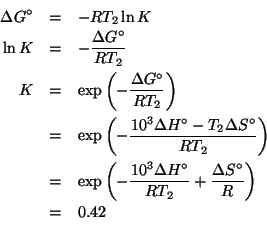
![]() di una lega
di una lega ![]() vengono ossidati completamente con
vengono ossidati completamente con
![]() : si ottengono
: si ottengono ![]() di
di ![]() , misurati a
, misurati a ![]() e
e
![]() . Calcolare la percentuale di
. Calcolare la percentuale di ![]() nella lega.
nella lega.
Dati:
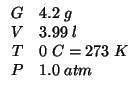
Altri simboli:
|
|
percentuale di |
| massa in |
|
| massa in |
|
| numero di moli di |
|
| numero di moli di |
|
| massa molare di |
|
| massa molare di |
|
| numero di moli di |
|
| costante dei gas:
|
La quantita' da determinare e':
Il problema consiste dunque nel trovare ![]() , visto che
, visto che ![]() e' dato.
e' dato.
![]() e' legato a
e' legato a ![]() dalla relazione:
dalla relazione:
Questa relazione, tuttavia, introduce ![]() come seconda
incognita. Si deve allora ricercare una seconda relazione indipendente
fra
come seconda
incognita. Si deve allora ricercare una seconda relazione indipendente
fra ![]() e
e ![]() .
.
Rimane ancora da utilizzare il dato relativo alla quantita' di idrogeno ottenuta.
Le equazioni chimiche che rappresentano l'ossidazione di ![]() e
e
![]() da parte di
da parte di ![]() sono:
sono:
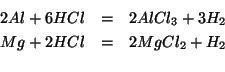
Dalla stechiometria delle reazioni segue:
Questa relazione puo' facilmente essere riscritta in termini delle masse
di ![]() e
e ![]() e del volume di
e del volume di ![]() prodotto:
prodotto:
La 1998-02-16:3:2 e la 1998-02-16:3:3 costituiscono un sistema
lineare di due equazioni nelle due incognite ![]() e
e
![]() . Moltiplicando la 1998-02-16:3:2 per
. Moltiplicando la 1998-02-16:3:2 per ![]() e sottraendola alla 1998-02-16:3:3 si ottiene:
e sottraendola alla 1998-02-16:3:3 si ottiene:
Infine, la 1998-02-16:3:4 viene sostituita nella 1998-02-16:3:1: