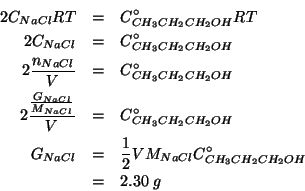Sapendo che il fosforo (![]() ) disproporziona in ambiente basico dando
fosfina (
) disproporziona in ambiente basico dando
fosfina (![]() , una sostanza gassosa in condizioni ordinarie) e
ione diidrogeno ipofosfito (
, una sostanza gassosa in condizioni ordinarie) e
ione diidrogeno ipofosfito (![]() ), calcolare il volume di una
soluzione di idrossido di bario
), calcolare il volume di una
soluzione di idrossido di bario
![]() necessaria per ottenere, per disproporzione del fosforo,
necessaria per ottenere, per disproporzione del fosforo, ![]() di fosfina, misurati a
di fosfina, misurati a ![]() e
e ![]() . Calcolare, inoltre,
la concentrazione finale di ione ipofosfito e la massa di fosforo
utilizzata.
. Calcolare, inoltre,
la concentrazione finale di ione ipofosfito e la massa di fosforo
utilizzata.
Dati:
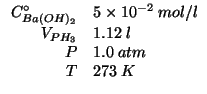
Altri simboli:
|
|
numero di moli di |
| numero di moli di ione |
|
| numero di moli di |
|
|
|
numero di moli di ione |
|
|
volume della soluzione di |
| massa di |
|
| massa molare di |
|
| costante dei gas:
|
La prima cosa da fare e' bilanciare l'equazione che descrive la reazione di disproporzione in esame. Applicando il metodo illustrato durante il corso si ha:
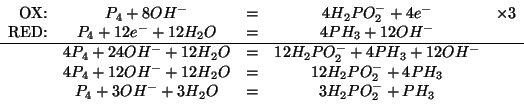
Ora l'equazione bilanciata fornisce i rapporti stechiometrici necessari.
Per rispondere al primo quesito, cominciamo con l'osservare che il
volume di soluzione di ![]() richiesto si puo' esprimere in
funzione del numero di moli e della concentrazione di
richiesto si puo' esprimere in
funzione del numero di moli e della concentrazione di ![]() :
:
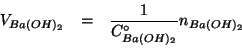
In base alla formula molecolare di ![]()
![]() puo' essere espresso in funzione di
puo' essere espresso in funzione di ![]() :
:
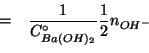
Dalla stechiometria della reazione segue:
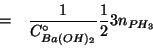
Infine, le moli di ![]() si ottengono applicando la legge del gas
ideale:
si ottengono applicando la legge del gas
ideale:
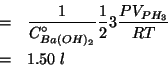
Alla fine della reazione, si ha una soluzione il cui volume e'
ovviamente quello della soluzione di ![]() utilizzata (si
trascurano eventuali variazioni di volume dovute al fosforo solido e
alla reazione). Per trovare la concentrazione finale di ione
utilizzata (si
trascurano eventuali variazioni di volume dovute al fosforo solido e
alla reazione). Per trovare la concentrazione finale di ione
![]() partiamo dalla definizione:
partiamo dalla definizione:
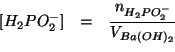
Chiaramente, le moli di ione ![]() sono esprimibili in
funzione di quelle di
sono esprimibili in
funzione di quelle di ![]() grazie alla stechiometria della
reazione:
grazie alla stechiometria della
reazione:
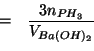
Infine, usiamo nuovamente la legge del gas ideale:
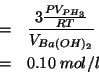
La massa di fosforo consumata nella reazione puo' essere espressa
facilmente in funzione delle moli di ![]() , ottenute ancora con la
legge del gas ideale:
, ottenute ancora con la
legge del gas ideale:
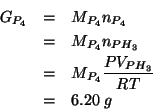
Per la reazione in fase gassosa:
si ha, a ![]() ,
,
![]() e
e
![]() . In un recipiente inizialmente vuoto
vengono introdotte
. In un recipiente inizialmente vuoto
vengono introdotte ![]() di
di ![]() e
e ![]() alla temperatura di
alla temperatura di
![]() . Quando il sistema ha raggiunto l'equilibrio, si trova che
la pressione totale all'interno del recipiente e' di
. Quando il sistema ha raggiunto l'equilibrio, si trova che
la pressione totale all'interno del recipiente e' di
![]() . Calcolare la pressione parziale di
. Calcolare la pressione parziale di ![]() all'equilibrio.
all'equilibrio.
(Si puo' assumere che
![]() e
e
![]() siano praticamente indipendenti dalla temperatura)
siano praticamente indipendenti dalla temperatura)
Dati:
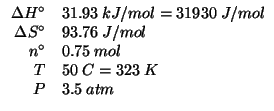
Altri simboli:
| numero di moli di |
|
| numero di moli totali presenti all'equilibrio | |
| costante di equilibrio della reazione | |
|
|
pressione parziale del componente
|
|
|
frazione molare del componente |
| costante dei gas:
|
La pressione parziale del componente ![]() all'equilibrio e' data
dalla sua frazione molare moltiplicata per la pressione totale:
all'equilibrio e' data
dalla sua frazione molare moltiplicata per la pressione totale:
![]() si trova impostando la trattazione dell'equilibrio nel modo
consueto (siccome
si trova impostando la trattazione dell'equilibrio nel modo
consueto (siccome ![]() e' inizialmente assente, la reazione deve
spostarsi necessariamente nel verso della sua formazione):
e' inizialmente assente, la reazione deve
spostarsi necessariamente nel verso della sua formazione):
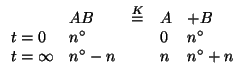
Le pressioni parziali (il sistema e' tutto in fase gassosa) dei componenti all'equilibrio devono soddisfare la legge dell'azione di massa:
Ciascuna pressione parziale puo' essere espressa in funzione della corrispondente frazione molare:
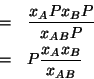
Ora, esprimiamo le frazioni molari in funzione dell'incognita ![]() ; a
questo scopo osserviamo che il numero totale di moli all'equilibrio si
ottiene semplicemente sommando le moli di ciascun componente:
; a
questo scopo osserviamo che il numero totale di moli all'equilibrio si
ottiene semplicemente sommando le moli di ciascun componente:
![]() :
:
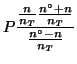 |
|||
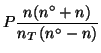 |
|||
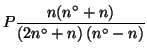 |
|||
(La soluzione col segno meno davanti al radicale va chiaramente scartata)
L'equazione ![]() fornisce
fornisce ![]() che puo'essere sostituito
nell'equazione
che puo'essere sostituito
nell'equazione ![]() per trovare il risultato.
per trovare il risultato.
Tuttavia, prima di procedere, bisogna conoscere ![]() , la costante di
equilibrio della reazione a
, la costante di
equilibrio della reazione a ![]() ; a questo scopo basta utilizzare
i dati termodinamici e la relazione che fornisce la dipendenza della
costante di equilibrio dalla temperatura:
; a questo scopo basta utilizzare
i dati termodinamici e la relazione che fornisce la dipendenza della
costante di equilibrio dalla temperatura:
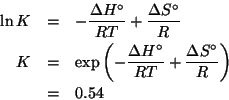
Sostituendo nell'equazione ![]() si ottiene:
si ottiene:
e sostituendo questo valore nell'equazione ![]() :
:
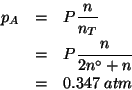
Calcolare la massa di cloruro di sodio che occorre sciogliere in
![]() di acqua per ottenere una soluzione isotonica ad una
soluzione
di acqua per ottenere una soluzione isotonica ad una
soluzione ![]() di alcol isopropilico
di alcol isopropilico
![]() alla stessa temperatura.
alla stessa temperatura.
(Trascurare la variazione di volume dovuta all'aggiunta del solido)
Dati:
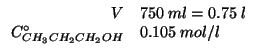
Altri simboli:
| concentrazione di |
|
| pressione osmotica della soluzione di |
|
| massa di |
|
| massa molare di |
|
| numero di moli di |
|
| costante dei gas | |
| temperatura |
La condizione di isotonicita' implica:
Utilizzando la relazione che lega la pressione osmotica alla
concentrazione, e ricordando che ![]() e' un elettrolita forte
completamente dissociato in ioni
e' un elettrolita forte
completamente dissociato in ioni ![]() e
e ![]() , si ha:
, si ha: