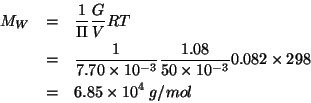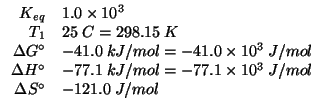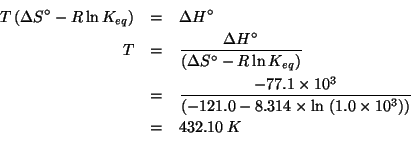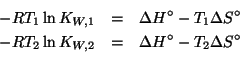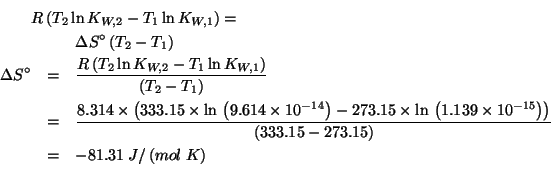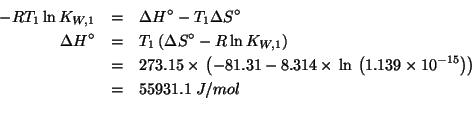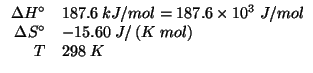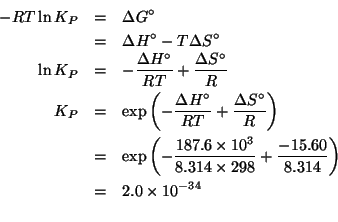(Questo esercizio vale 3 punti)
Applicando il metodo visto durante il corso si ha:
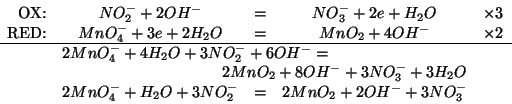
(Questo esercizio vale 3 punti)
Dati:

Altri simboli:
| numero di moli di permanganato | |
|
|
numero di moli di acido ossalico |
|
|
massa molare dell'acido ossalico: |
Per prima cosa scriviamo e bilanciamo l'equazione che rappresenta la
reazione. Ovviamente, si tratta di una reazione redox (che, per altro,
abbiamo fatto in pratica nel corso di laboratorio).
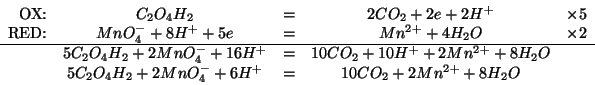
Dall'equazione bilanciata si vede che:
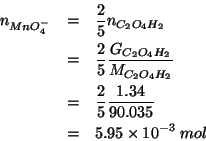
Il volume di soluzione che contiene il numero di moli di permanganato su scritto e' dato da:
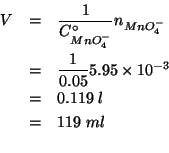
![]() di esacianoferrato (III) di ammonio solido vengono fatti
reagire con una soluzione di acido solforico
di esacianoferrato (III) di ammonio solido vengono fatti
reagire con una soluzione di acido solforico ![]() che
contiene un eccesso di acido pari al
che
contiene un eccesso di acido pari al ![]() (in moli) della
quantita' stechiometrica richiesta.
(in moli) della
quantita' stechiometrica richiesta.
- (a)
- calcolate il volume di soluzione di acido solforico che e' stato utilizzato
- (b)
- calcolate la concentrazione di solfato di ammonio e solfato ferrico prodotti dalla reazione
(Questo esercizio vale 3 punti)
Dati:
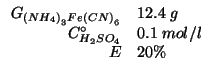
Altri simboli:
|
|
massa molare di
|
|
|
numero di moli di
|
| numero di moli di |
|
| volume di soluzione di |
|
|
|
numero di moli di
|
|
|
numero di moli di
|
|
|
concentrazione molare di
|
|
|
concentrazione molare di
|
Per prima cosa troviamo il numero di moli di
![]() :
:
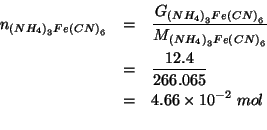
Le moli di acido solforico utilizzate (tenendo conto che devono essere
in eccesso del ![]() rispetto alla quantita' stechiometrica)
saranno percio':
rispetto alla quantita' stechiometrica)
saranno percio':
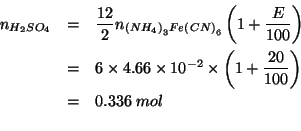
e quindi il volume di soluzione cercato e':
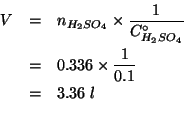
Conoscendo il numero di moli di
![]() che hanno reagito
(
che hanno reagito
(
![]() e' ovviamente il reagente
limitante, visto che
e' ovviamente il reagente
limitante, visto che ![]() e' stato usato in eccesso), si trova
subito il numero di moli di
e' stato usato in eccesso), si trova
subito il numero di moli di
![]() e quello di
e quello di
![]() prodotti. Dalla stechiometria
dell'equazione bilanciata:
prodotti. Dalla stechiometria
dell'equazione bilanciata:
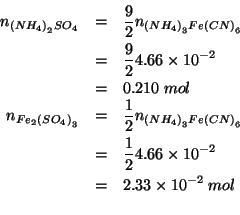
Conoscendo il volume ![]() della soluzione (che coincide con il volume
di soluzione di
della soluzione (che coincide con il volume
di soluzione di ![]() aggiunto, dato che
aggiunto, dato che
![]() era solido), le
concentrazioni sono ricavate immediatamente:
era solido), le
concentrazioni sono ricavate immediatamente:
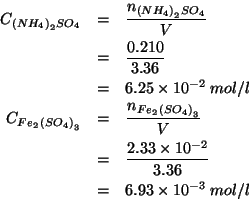
(Questo esercizio vale 3 punti)
Il numero di ossidazione del cloro nelle tre specie chimiche e':
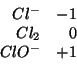
Possiamo quindi considerare le seguenti due coppie redox che condividono un membro (questa e' la condizione per avere una reazione di disproporzione):
La reazione di disproporzione si ottiene facendo reagire la coppia
![]() nel verso della riduzione e la coppia
nel verso della riduzione e la coppia ![]() nel verso della ossidazione: in tal modo, al primo membro della
reazione redox globale comparira' solo
nel verso della ossidazione: in tal modo, al primo membro della
reazione redox globale comparira' solo ![]() .
.
Applicando il metodo visto durante il corso e tenendo presente che la reazione avviene in ambiente basico si ha:
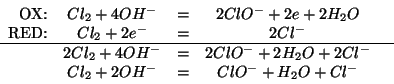
(Questo esercizio vale 3 punti)
Dati:
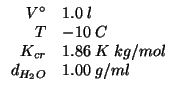
Altri simboli:
|
|
massa molare del glicole etilenico:
|
| molalita' | |
|
|
massa del glicole etilenico in |
| massa dell'acqua in |
|
|
|
numero di moli di glicole etilenico |
Scriviamo la legge dell'abbassamento crioscopico:
In pratica, dobbiamo determinare ![]() in modo che sia:
in modo che sia:
![]() .
.
Quindi:
Ora esprimiamo ![]() in funzione della quantita' in grammi di glicole
e della sua massa molare:
in funzione della quantita' in grammi di glicole
e della sua massa molare:
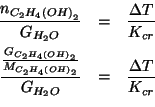
Riarrangiando si ottiene:
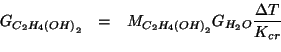
Osserviamo infine che, essendo
![]() , massa e volume
di un campione d'acqua hanno lo stesso valore numerico. Quindi:
, massa e volume
di un campione d'acqua hanno lo stesso valore numerico. Quindi:
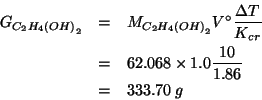
(Questo esercizio vale 3 punti)
Dati:
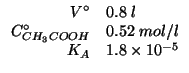
Altri simboli:
|
|
massa molare dell'acetato di sodio:
|
|
|
numero di moli di |
|
|
numero di moli di |
Durante il corso abbiamo visto che il ![]() di un tampone costituito
da un acido debole e dalla sua base coniugata puo' essere scritto
nella forma:
di un tampone costituito
da un acido debole e dalla sua base coniugata puo' essere scritto
nella forma:
Nel caso in esame, l'acido debole e' l'acido acetico e la sua base coniugata e' lo ione acetato, che si forma in seguito alla dissociazione completa dell'acetato di sodio:
L'espressione su scritta puo' essere riarrangiata per trovare
![]() :
:
Le moli di acido acetico sono ottenute immediatamente dalla sua concentrazione e dal volume di soluzione. Quindi:
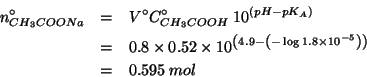
Per trovare la quantita' di acetato di sodio in grammi basta moltiplicare il numero di moli per la massa molare:
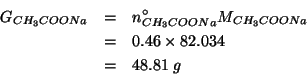
(Questo esercizio vale 3 punti)
Per determinare la geometria molecolare cominciamo con lo scrivere la formula di Lewis dello ione molecolare.
| Elettroni di valenza | |
| carica | 1 |
| totale | |
![\begin{displaymath}
\left[\mbox{\rule{2em}{0mm}}
\begin{xy}
<1em,0em>:
c*+{I};p...
...*\dir{}?<*\dir{\vert},
\end{xy}\mbox{\rule{2em}{0mm}}\right]^-
\end{displaymath}](img90.gif)
Si puo' facilmente verificare che questa e' la formula di risonanza piu' stabile. Tuttavia, la particolare formula di risonanza che si considera (purche' corretta!) non ha importanza, poiche' siamo interessati alla geometria molecolare e all'ibridazione dell'atomo centrale, che non dipendono dalla particolare formula di risonanza considerata.
Dalla formula di Lewis si ricava subito che il numero di coppie
strutturali e' ![]() . Da cio' segue che la geometria delle coppie
strutturali e' bipiramidale trigonale e l'ibridazione dell'atomo di
iodio e'
. Da cio' segue che la geometria delle coppie
strutturali e' bipiramidale trigonale e l'ibridazione dell'atomo di
iodio e' ![]() .
.
Le tre coppie di non legame si disporranno ad occupare tutte e tre le posizioni equatoriali (meno ingombrate rispetto a quelle assiali): ne segue che la geometria molecolare sara' di tipo lineare.
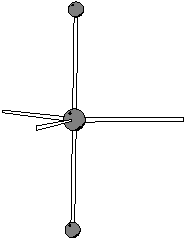 |
|
| geometria delle coppie strutturali | geometria molecolare |
(Questo esercizio vale 3 punti)
Dati:
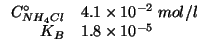
Altri simboli:
| prodotto ionico dell'acqua:
|
![]() e' un sale costituito dall'acido coniugato di una base
debole (lo ione ammonio) e dalla base coniugata di un acido forte (lo
ione cloruro). Posto in soluzione acquosa esso si dissocia
completamente e lo ione ammonio dara' un'apprezzabile idrolisi acida
(mentre le proprieta' basiche dello ione cloruro sono
trascurabili). Si tratta quindi di calcolare il
e' un sale costituito dall'acido coniugato di una base
debole (lo ione ammonio) e dalla base coniugata di un acido forte (lo
ione cloruro). Posto in soluzione acquosa esso si dissocia
completamente e lo ione ammonio dara' un'apprezzabile idrolisi acida
(mentre le proprieta' basiche dello ione cloruro sono
trascurabili). Si tratta quindi di calcolare il ![]() di una
soluzione contenente l'acido debole
di una
soluzione contenente l'acido debole ![]() in concentrazione
iniziale pari a quella del sale:
in concentrazione
iniziale pari a quella del sale:
Durante il corso si e' visto che la concentrazione di ioni idronio in
una soluzione contenente un acido debole ![]() di costante di
ionizzazione acida
di costante di
ionizzazione acida ![]() in concentrazione iniziale pari a
in concentrazione iniziale pari a
![]() e' data da:
e' data da:
Nel caso presente la formula diventa:
dove ![]() e' la costante di ionizzazione acida dello ione
ammonio. Quest'ultima si ottiene facilmente sapendo che deve valere:
e' la costante di ionizzazione acida dello ione
ammonio. Quest'ultima si ottiene facilmente sapendo che deve valere:
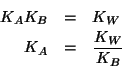
Quindi:
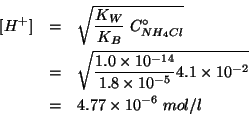
e:
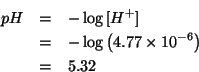
Come c'era da aspettarsi, il ![]() della soluzione risulta acido.
della soluzione risulta acido.

Calcolate la massa atomica geonormale del cromo con sette cifre decimali.
(Questo esercizio vale 3 punti)
Dati:
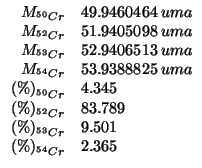
Altri simboli:
| massa atomica geonormale del cromo |
Applicando la formula vista durante il corso:
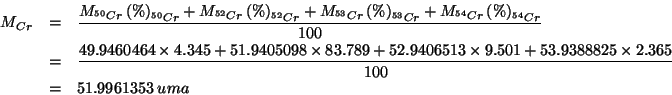
(Questo esercizio vale 3 punti)
Dati:
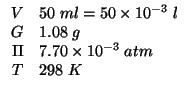
Altri simboli:
| numero di moli di albumina | |
| molarita' della soluzione | |
| costante dei gas:
|
|
| la massa molare dell'albumina in |
Scriviamo la legge della pressione osmotica:
La molarita' della soluzione puo' essere facilmente espressa in funzione della quantita' in grammi di albumina e della sua massa molare:
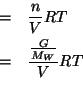
Risolvendo rispetto alla massa molare si ottiene: