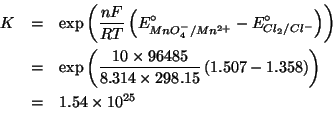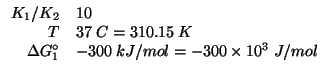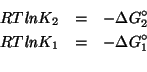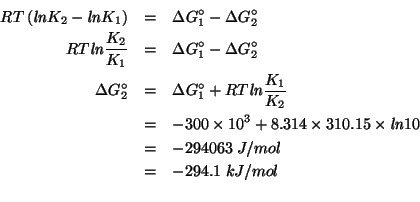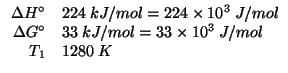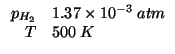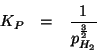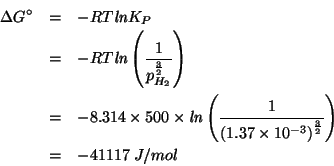Applicando il metodo visto durante il corso:
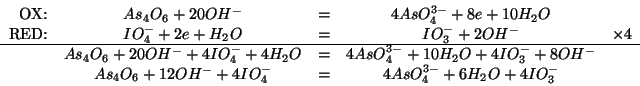
(Suggerimento: indicate con ![]() la massa in
la massa in ![]() di
di ![]() e con
e con
![]() quella di
quella di ![]() . Innanzitutto dovra' essere:
. Innanzitutto dovra' essere:
![]() . Bilanciate le due equazioni per l'ossidazione dei due
metalli: il numero totale di moli di idrogeno prodotto e' la somma
del numero di moli di idrogeno prodotte nelle due reazioni. Queste,
a loro volta, sono in relazione con il numero di moli dei due
metalli tramite la stechiometria. Riuscirete cosi' a scrivere una
seconda relazione che lega
. Bilanciate le due equazioni per l'ossidazione dei due
metalli: il numero totale di moli di idrogeno prodotto e' la somma
del numero di moli di idrogeno prodotte nelle due reazioni. Queste,
a loro volta, sono in relazione con il numero di moli dei due
metalli tramite la stechiometria. Riuscirete cosi' a scrivere una
seconda relazione che lega ![]() e
e ![]() e quindi vi resta da
risolvere un semplice sistema lineare di due equazioni.)
e quindi vi resta da
risolvere un semplice sistema lineare di due equazioni.)
Dati:
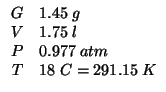
Altri simboli:
| massa molare del magnesio: |
|
| massa molare dell'alluminio: |
|
| costante dei gas:
|
|
| numero di moli di magnesio | |
| numero di moli di alluminio | |
| numero di moli di idrogeno prodotte dall'ossidazione del magnesio | |
| numero di moli di idrogeno prodotte dall'ossidazione dell'alluminio | |
| numero totale di moli di idrogeno prodotto |
Seguendo il suggerimento, indicando con ![]() la massa in grammi di
la massa in grammi di
![]() e con
e con ![]() quella di
quella di ![]() si ha:
si ha:
Ora scriviamo le due equazioni redox bilanciate. Data la loro semplicita', non serve ricorrere alla scomposizione in semieqauzioni.
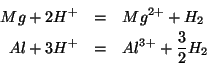
Tramite la stechiometria delle due equazioni bilanciate possiamo esprimere il numero di moli di idrogeno prodotto da ciascuna reazione in funzione del numero di moli del metallo:
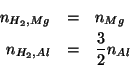
I numeri di moli dei metalli sono esprimibili in funzione delle rispettive masse in grammi e delle masse molari:
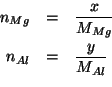
Quindi:
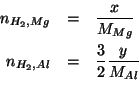
Come suggerito, il numero totale di moli di idrogeno prodotto e' la somma dei numeri di moli prodotti in ciascuna reazione:
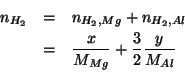
D'altro canto, ![]() e' esprimibile anche tramite la legge dei
gas ideali, utilizzando i dati di volume, pressione e temperatura:
e' esprimibile anche tramite la legge dei
gas ideali, utilizzando i dati di volume, pressione e temperatura:
e quindi:
che e' la seconda relazione cercata fra ![]() e
e ![]() .
.
Ora si tratta di risolvere il sistema:
Moltiplicando la seconda equazione per ![]() e sottraendola
dalla prima si ottiene:
e sottraendola
dalla prima si ottiene:
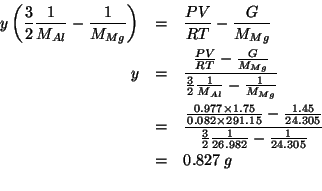
La percentuale in massa di alluminio nella miscela e':
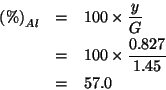
Ovviamente, per il magnesio si ha:
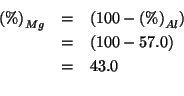
La costante di ionizzazione dell'acido acetico vale
![]() .
.
Dati:
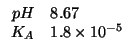
Altri simboli:
|
|
concentrazione iniziale di ione acetato |
|
|
concentrazione iniziale del sale |
| costante di ionizzazione basica dello ione acetato | |
| prodotto ionico dell'acqua:
|
L'acetato di bario e' un sale costituito dalla base coniugata
dell'acido acetico e dallo ione di un metallo alcalino
terroso. Quest'ultimo ha proprieta' acide trascurabili e quindi il
![]() della soluzione e' dovuto all'idrolisi basica dello ione
acetato, che si forma in seguito alla completa dissociazione del sale:
della soluzione e' dovuto all'idrolisi basica dello ione
acetato, che si forma in seguito alla completa dissociazione del sale:
Durante il corso e' stata ricavata la formula che da' il ![]() per
un'idrolisi basica:
per
un'idrolisi basica:
![\begin{eqnarray*}
pOH&=&-\log\left(\left[OH^-\right]\right)\\
&=&-\log\left(\sqrt{K_B\times{}C^\circ_{CH_3COO^-}}\right)\\
\end{eqnarray*}](img52.gif)
La costante di ionizzazione basica dello ione acetato si trova conoscendo la costante di ionizzazione acida dell'acido acetico e sapendo che:
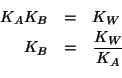
Per la concentrazione iniziale di acetato, si deve tenere presente la stechiometria della dissociazione dell'acetato di bario:
da cui:
Quindi, sostituendo piu' sopra:
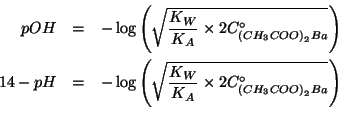
L'equazione ottenuta contiene la concentrazione del sale come unica incognita. Allora:
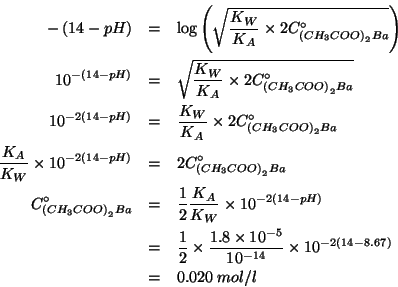
Dati:
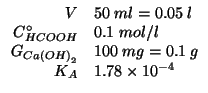
Altri simboli:
| costante di equilibrio della reazione fre acido formico e ione ossidrile | |
| costante di ionizzazione basica dello ione formiato | |
| prodotto ionico dell'acqua:
|
|
|
|
concentrazione iniziale di ione ossidrile |
|
|
concentrazione iniziale di idrossido di calcio |
|
|
numero di moli di idrossido di calcio |
|
|
massa molare dell'idrossido di calcio: |
Prima dell'aggiunta dell'idrossido, il problema e' quello di trovare
il ![]() di una soluzione contenente una concentrazione data di un
acido debole. Durante il corso e' stata ricavata la formula che
fornisce la risposta:
di una soluzione contenente una concentrazione data di un
acido debole. Durante il corso e' stata ricavata la formula che
fornisce la risposta:
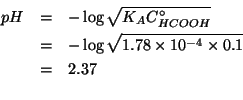
Dopo l'aggiunta dell'idrossido siamo nel caso di una soluzione che contiene un acido debole e una base forte. La reazione che avviene in soluzione e':
Questa reazione si puo' considerare praticamente completa; infatti, essa e' l'inversa della ionizzazione basica dello ione formiato e quindi:
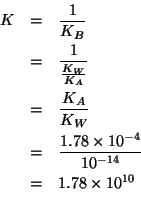
Potendo considerare la reazione completa, bisogna vedere qual'e' il reagente limitante.
La concentrazione iniziale degli ioni ossidrile (trascurando, come al solito, l'autoionizzazione dell'acqua) e' ottenuta considerando la stechiometria della dissociazione dell'idrossido di calcio:
Quindi:
D'altro canto:
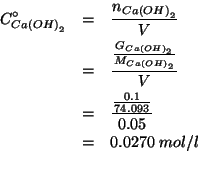
Sostituendo piu' sopra:
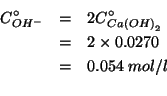
Gli ioni ossidrile sono in difetto stechiometrico e quindi alla fine
della reazione la soluzione conterra' ione formiato in concentrazione
uguale alla concentrazione iniziale degli ioni ossidrile e acido
formico in concentrazione pari a
![]() :
si tratta dunque di una soluzione tampone per la quale e' stata
ricavata la formula che fornisce il
:
si tratta dunque di una soluzione tampone per la quale e' stata
ricavata la formula che fornisce il ![]() :
:
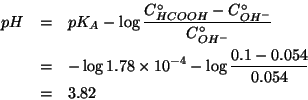
Dati:
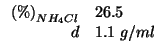
Altri simboli:
| massa di cloruro di ammonio | |
| numero di moli di cloruro di ammonio | |
| volume della soluzione | |
| molarita' | |
| massa di acqua | |
| molalita' | |
| numero di moli di acqua | |
| massa molare dell'acqua: |
|
| massa molare del cloruro d'ammonio: |
La concentrazione di una soluzione non dipende dalla quantita' di
soluzione considerata e quindi possiamo basarci sulla quantita' di
soluzione che piu' ci conviene. Consideriamo allora ![]() di
soluzione.
di
soluzione.
La massa di cloruro d'ammonio contenuta in ![]() di soluzione e'
data da:
di soluzione e'
data da:
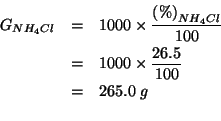
Tale massa equivale al seguente numero di moli:
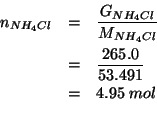
Il volume di ![]() di soluzione e':
di soluzione e':
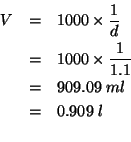
Allora, per la molarita':
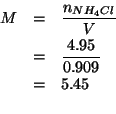
La massa di acqua contenuta in ![]() di soluzione e':
di soluzione e':
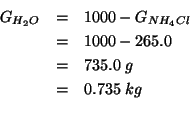
Allora, per la molalita':
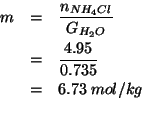
Il numero di moli di acqua contenuto in ![]() di soluzione e':
di soluzione e':
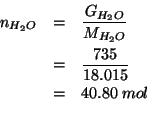
Per la frazione molare:
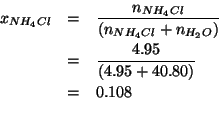
Dati:
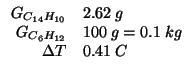
Altri simboli:
| costante ebullioscopica del cicloesano in
|
|
| molalita' | |
|
|
numero di moli di antracene |
|
|
massa molare dell'antracene:
|
Applicando la formula dell'innalzamento ebullioscopico:
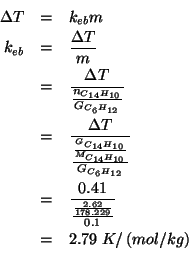
Applichiamo il metodo per la costruzione delle formule di Lewis illustrato durante il corso:
| Elettroni di valenza | |
| carica | |
| totale | |
Ponendo l'atomo di boro (meno elettronegativo) al centro si ottiene:
![\begin{displaymath}
\left[
\begin{xy}
<1em,0em>:
*+{B},c=''B'';
p+/l2em/*+{F},*...
...{\vert},
p+/r0.1em/**\dir{}?<*\dir{\vert},
\end{xy}\right]^{-}
\end{displaymath}](img120.gif)
Il boro appartiene al secondo periodo e quindi non puo' avere valenza espansa: quella scritta e' dunque l'unica possibilita'.
Dalla formula di Lewis si vede che ci sono ![]() coppie strutturali:
la geometria delle coppie strutturali sara' quindi tetraedrica, come
vuole il modello VSEPR.
coppie strutturali:
la geometria delle coppie strutturali sara' quindi tetraedrica, come
vuole il modello VSEPR.
Non essendoci coppie di non legame attorno all'atomo di boro, la geometria molecolare coincide con quella delle coppie strutturali:
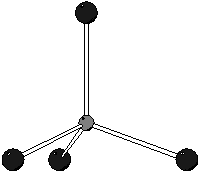
Essendo la geometria delle coppie strutturali tetraedrica, il boro
sara' ibridizzato ![]() .
.

Ricavatene la formula molecolare e la formula minima.
Dati:

Altri simboli:
| massa di |
|
| massa di |
|
| massa di |
|
| massa molare del |
|
| massa molare dell' |
|
| massa molare dell' |
|
| numero di moli di |
|
| numero di moli di |
|
| numero di moli di |
Consideriamo una massa di composto pari alla sua massa molare. La massa di ciascuno degli elementi costituenti contenuta in una massa di composto pari alla sua massa molare e':
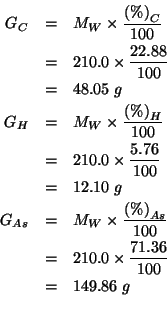
Queste masse corrispondono ai seguenti numeri di moli:
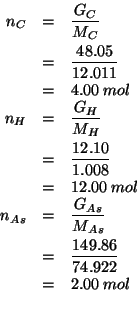
Essendo questi i numeri di moli di ![]() ,
, ![]() e
e ![]() contenuti in
contenuti in
![]() di composto, ne segue che la formula molecolare e':
di composto, ne segue che la formula molecolare e':
La formula minima, per convenzione, utilizza i numeri interi piu' piccoli possibile. Allora la formula minima sara':
Per ossidare l'ossalato contenuto in ![]() di una soluzione al
di una soluzione al
![]() in massa (densita':
in massa (densita': ![]() ) sono stati necessari
) sono stati necessari
![]() di soluzione di permanganato. Calcolate la molarita' della
soluzione di permanganato.
di soluzione di permanganato. Calcolate la molarita' della
soluzione di permanganato.
Dati:
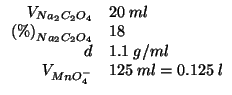
Altri simboli:
| numero di moli di permanganato | |
|
|
numero di moli di ossalato |
|
|
massa di ossalato si sodio in |
|
|
massa molare dell'ossalato di sodio:
|
|
|
massa della soluzione di ossalato in
|
| molarita' della soluzione di permanganato |
Innanzitutto scriviamo l'equazione bilanciata relativa alla reazione
fra permanganato e ossalato (ovviamente, l'ossalato di sodio, in
quanto sale, e' completamente dissociato in ioni ![]() , spettatori,
e ioni
, spettatori,
e ioni ![]() ). Col consueto metodo discusso durante il corso
si ha:
). Col consueto metodo discusso durante il corso
si ha:
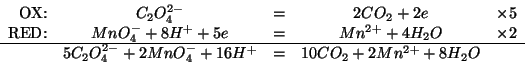
Dalla stechiometria della reazione si deduce immediatamente:
Per trovare il numero di moli di ossalato, sfruttando i dati a disposizione:
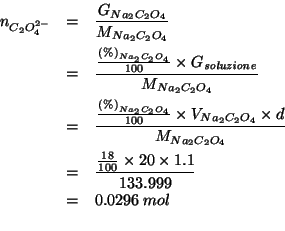
Quindi:
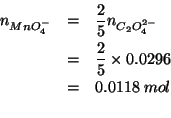
e la molarita' della soluzione di permanganato e':
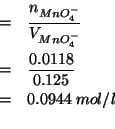
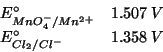
Dati:

Altri simboli:
| numero di elettroni scambiati nella reazione | |
| costante di Faraday: |
|
| costante dei gas:
|
Prima di tutto scriviamo l'equazione bilanciata per la reazione in questione:
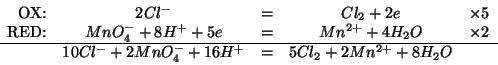
La costante di equilibrio di una reazione redox e' in relazione con i potenziali standard di riduzione delle due coppie implicate tramite:
Sostituendo: