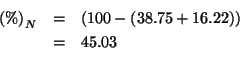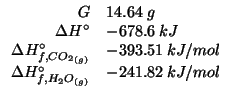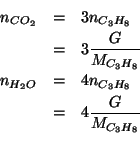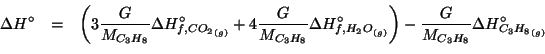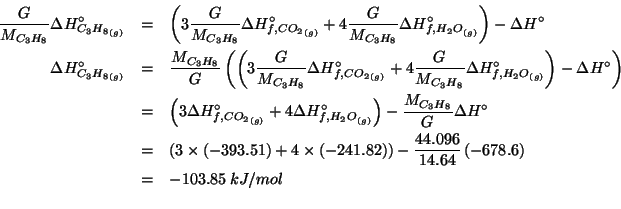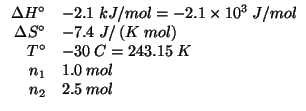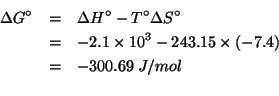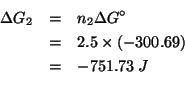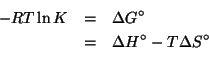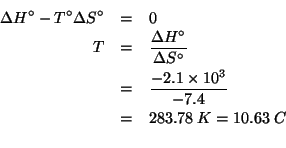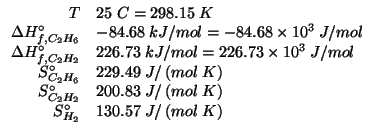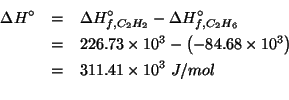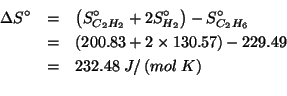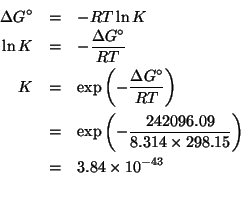Dati:
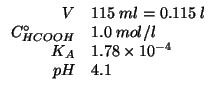
Altri simboli:
| costante di equilibrio della reazione fra acido formico e ioni ossidrile | |
| costante di ionizzazione basica dello ione formiato | |
| prodotto ionico dell'acqua:
|
|
|
|
concentrazione iniziale di ioni ossidrile |
|
|
numero di moli iniziale di ioni ossidrile |
|
|
numero di moli iniziale di idrossido di calcio |
|
|
massa in grammi di idrossido di calcio |
|
|
massa molare dell'idrossido di calcio: |
L'idrossido di calcio e' completamente dissociato secondo l'equazione:
Gli ioni ossidrile reagiscono con l'acido formico secondo:
La costante di equilibrio di questa reazione e' molto grande. Infatti essa e' l'inversa della ionizzazione basica dello ione formiato e quindi:
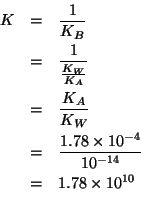
Essendo
![]() , la reazione fra acido formico e ioni
ossidrile si puo' considerare completa. Chiaramente, se si vuole
ottenere una soluzione tampone, lo ione ossidrile deve essere aggiunto
in difetto. Allora le concentrazioni delle specie implicate alla fine
della reazione saranno:
, la reazione fra acido formico e ioni
ossidrile si puo' considerare completa. Chiaramente, se si vuole
ottenere una soluzione tampone, lo ione ossidrile deve essere aggiunto
in difetto. Allora le concentrazioni delle specie implicate alla fine
della reazione saranno:
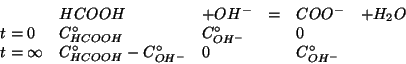
La formula che da' il ![]() della soluzione tampone cosi' ottenuta e'
stata ricavata durante il corso:
della soluzione tampone cosi' ottenuta e'
stata ricavata durante il corso:
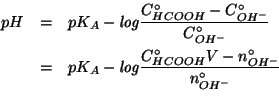
L'equazione contiene
![]() come unica incognita: non
resta che risolverla.
come unica incognita: non
resta che risolverla.
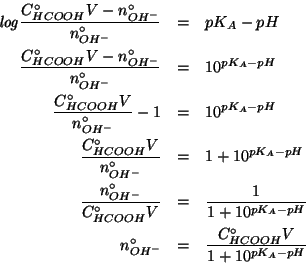
Dall'equazione di dissociazione dell'idrossido di calcio si vede che:
e allora:
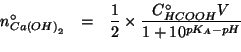
Infine, per trovare la massa in grammi:
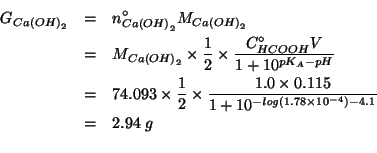
Dati:
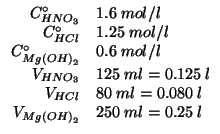
Altri simboli:
|
|
numero di moli iniziale di |
| numero di moli iniziale di |
|
|
|
numero di moli iniziale di
|
| numero di moli iniziale di ioni idronio | |
|
|
numero di moli iniziale di ioni ossidrile |
| costante di equilibrio della reazione fra ioni idronio e ioni ossidrile |
L'acido nitrico e l'acido cloridrico sono entrambi acidi forti; l'idrossido di magnesio e' una base forte. Tutti i composti mescolati sono quindi completamente dissociati:
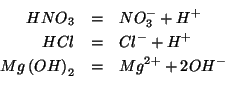
All'atto del mescolamento si avra' quindi la reazione fra gli ioni idronio provenienti dai due acidi e gli ioni ossidrile provenieneti dall'idrossido:
La costante di equilibrio di questa reazione e', ovviamente:
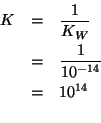
La reazione si puo' pertanto assumere completa. Dobbiamo allora vedere qual'e' il reagente limitante. Per comodita', consideriamo il numero di moli di ciascun reagente.
Il numero di moli di ioni idronio e' la somma di quello degli ioni idronio provenienti dall'acido nitrico e di quello degli ioni idronio provenienti dall'acido cloridrico:
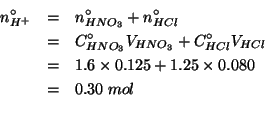
Il numero di moli di ioni ossidrile e' doppio del numero di moli di idrossido di magnesio (guardate l'equazione che descrive la sua dissociazione):
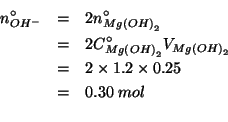
Troviamo che i due reagenti (![]() e
e ![]() ) sono in rapporto
stechiometrico. Allora, indicando con
) sono in rapporto
stechiometrico. Allora, indicando con ![]() la concentrazione
comune (di cui non ci interessa calcolare il valore) si ha:
la concentrazione
comune (di cui non ci interessa calcolare il valore) si ha:
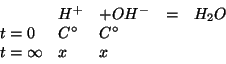
Inserendo le concentrazioni di equilibrio nella legge dell'azione di massa si ottiene:
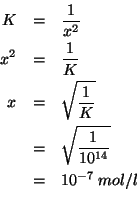
come si poteva facilmente prevedere.
Il ![]() della soluzione sara' dunque uguale a quello dell'acqua pura:
della soluzione sara' dunque uguale a quello dell'acqua pura:
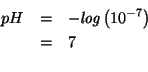
Dati:
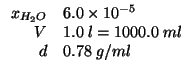
| massa di acqua in |
|
| massa di |
|
| massa molare dell'acqua: |
|
| massa molare del metano: |
|
|
|
massa di acqua in |
|
|
massa di metano in |
| massa in |
|
|
|
numero di moli di acqua contenuto in una soluzione
tale che:
|
|
|
numero di moli di metano contenuto in una soluzione
tale che:
|
| frazione in massa dell'acqua |
Per rispondere al quesito posto dal problema, trasformiamo la frazione molare data nella corrispondente frazione in massa.
E' chiaro che la frazione in massa cercata non dipende dalla quantita' di soluzione considerata e quindi, per trasformare la frazione molare nella corrispondente frazione in massa, siamo liberi di ragionare su una quantita' di soluzione che sia piu' conveniente possibile.
Consideriamo allora una soluzione di acqua in metano tale che contenga
un numero totale di moli pari a ![]() :
:
Essendo data la frazione molare dell'acqua, ovviamente sara':
e quindi le moli di metano saranno:
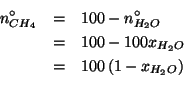
La massa di acqua contenuta in tale soluzione e':
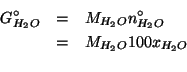
Analogamente, la massa di metano e':
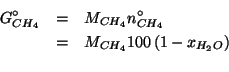
La massa dell'intera soluzione e':
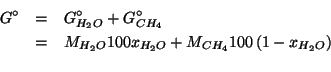
Allora, la frazione in massa dell'acqua cercata e':
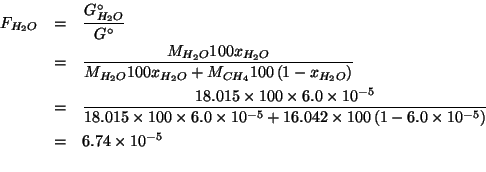
Infine, avendo trovato la frazione in massa dell'acqua, e' immediato ottenere la massa di acqua contenuta in un litro di soluzione.
La massa in ![]() di un litro di soluzione e':
di un litro di soluzione e':
e quindi:
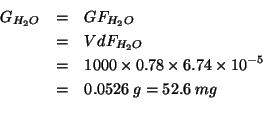
Dati:
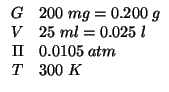
Altri simboli:
| costante dei gas:
|
|
| numero di moli del composto | |
| massa in grammi del composto | |
| la massa molare incognita, in |
Cominciamo a scrivere la formula della pressione osmotica:
Siccome il composto e' non elettrolita, la concentrazione colligativa coincide con la concentrazione molare formale. Quindi:
Il numero di moli del composto puo' essere espresso in funzione della massa in grammi e della massa molare cercata:
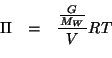
Nell'equazione ottenuta la massa molare e' l'unica incognita. Allora:
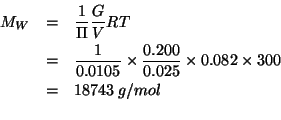
Una mole di questa macromolecola pesa quasi ![]() !
!
Quale volume di gas (stibina) (misurato a ![]() e
e ![]() )
verra' prodotto da
)
verra' prodotto da ![]() di
di ![]() che reagiscono con un
eccesso di
che reagiscono con un
eccesso di ![]() ? Quale concentrazione molare di cloruro di zinco si
realizzera' in un volume totale di soluzione pari a
? Quale concentrazione molare di cloruro di zinco si
realizzera' in un volume totale di soluzione pari a ![]() ?
?
Dati:
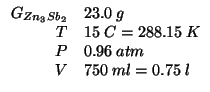
Altri simboli:
| costante dei gas:
|
|
| numero di moli di |
|
|
|
numero di moli di |
|
|
massa molare di |
| numero di moli di |
|
| concentrazione molare di |
Dalla stechiometria della reazione e dal fatto che ![]() e' il
reagente limitante si ricava:
e' il
reagente limitante si ricava:
ovvero:
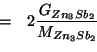
Il volume occupato da queste moli di gas nelle condizioni di temperatura e pressione date si ricava applicando la legge dei gas ideali:
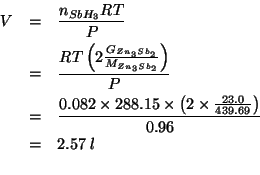
Sempre guardando la stechiometria della reazione, si ricava immediatamente:
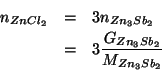
Se questo numero di moli e' sciolto nel volume di soluzione dato, la concentrazione molare sara':
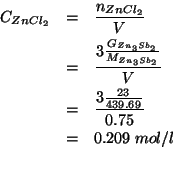
La costante crioscopica dell'acqua e'
![]() .
.
Dati:
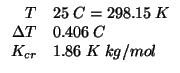
Altri simboli:
| pressione osmotica in |
|
| concentrazione molare colligativa | |
| costante dei gas:
|
|
| molalita' colligativa |
Siccome la soluzione di ![]() data e' isotonica (cioe' ha la stessa
pressione osmotica) con il contenuto degli eritrociti, per il calcolo
possiamo basarci sulla soluzione di
data e' isotonica (cioe' ha la stessa
pressione osmotica) con il contenuto degli eritrociti, per il calcolo
possiamo basarci sulla soluzione di ![]() .
.
La concentrazione colligativa del cloruro di sodio non e' data, ma possiamo ricavare facilmente la sua molalita' colligativa dai dati relativi all'abbassamento crioscopico:
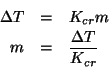
Il testo del problema ci consente di assumere che il valore trovato coincida con la molarita' colligativa, che possiamo cosi' inserire nella formula della pressione osmotica:
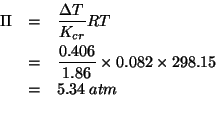
Applichiamo il metodo per la costruzione delle formule di Lewis illustrato durante il corso:
| Elettroni di valenza | |
| carica | |
| totale | |
Ponendo l'atomo di azoto (meno elettronegativo) al centro si ottiene:
L'atomo centrale non e' circondato da ![]() elettroni e quindi
impegneremo coppie solitarie degli atomi terminali per formare legami
elettroni e quindi
impegneremo coppie solitarie degli atomi terminali per formare legami
![]() con l'atomo centrale. Sulla carta, ci sono tre possibilita':
con l'atomo centrale. Sulla carta, ci sono tre possibilita':
La stabilita' delle tre diverse formule di risonanza puo' essere giudicata sulla base della carica atomica formale:
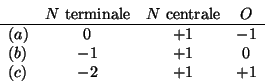
Dall'analisi delle cariche atomiche formali si deduce che la struttura
![]() sara' la meno stabile, perche' possiede le cariche maggiori mentre
la struttura
sara' la meno stabile, perche' possiede le cariche maggiori mentre
la struttura ![]() e' piu' stabile della
e' piu' stabile della ![]() perche' la carica
negativa e' localizzata sull'atomo piu' elettronegativo. L'ordine di
stabilita' crescente e' dunque:
perche' la carica
negativa e' localizzata sull'atomo piu' elettronegativo. L'ordine di
stabilita' crescente e' dunque:
Dalle formule di Lewis si vede che l'atomo centrale e' circondato da
![]() coppie strutturali: la geometria delle coppie strutturali sara'
quindi lineare, come vuole il modello VSEPR.
coppie strutturali: la geometria delle coppie strutturali sara'
quindi lineare, come vuole il modello VSEPR.
Non essendoci coppie di non legame attorno all'atomo di azoto, la geometria molecolare coincide con quella delle coppie strutturali:
Infine, essendo la geometria delle coppie strutturali lineare, l'azoto
sara' ibridizzato ![]() .
.
Usando il metodo imparato durante il corso, bilanciatela in due modi diversi (ma che portano, ovviamente, allo stesso risultato).
Come tutte le reazioni redox, anche questa si puo' scomporre in due semiequazioni relative a due coppie redox. La particolarita', tuttavia, e' che la scelta delle coppie redox non e' univoca. Potremmo infatti ripartire i partecipanti cosi':
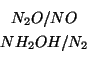
oppure cosi':
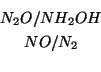
Chiaramente, ai fini del bilanciamento, non ha nessuna importanza come si scelgono le coppie redox.
Con la prima scelta, applicando il consueto metodo, si ha:
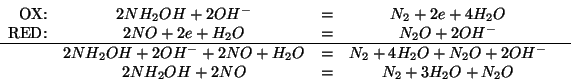
Con la seconda scelta si ha:
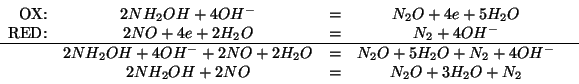
per la quale la costante di equilibrio a ![]() vale
vale
![]() . Calcolate la pressione parziale di equilibrio del fosgene in
un recipiente in cui sia stata introdotta inizialmente una miscela
costituita da
. Calcolate la pressione parziale di equilibrio del fosgene in
un recipiente in cui sia stata introdotta inizialmente una miscela
costituita da ![]() di cloro e
di cloro e ![]() di monossido
di carbonio a
di monossido
di carbonio a ![]() .
.
Dati:
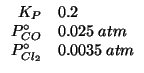
La costante di equilibrio della reazione non e' ne' molto grande ne' molto piccola e quindi non si possono fare delle semplificazioni.
Impostiamo il trattamento dell'equilibrio con la tabella vista durante il corso. Siccome la reazione avviene a volume e temperatura costante, numeri di moli e pressioni parziali sono proporzionali e quindi possiamo usare direttamente le pressioni parziali.
Scegliendo la pressione parziale di equilibrio del fosgene come incognita, si ha:
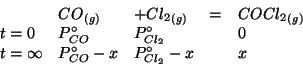
Come di consueto, inseriamo le pressioni parziali di equilibrio nella legge dell'azione di massa:
Non resta che risolvere l'equazione di secondo grado ottenuta.
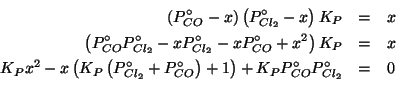
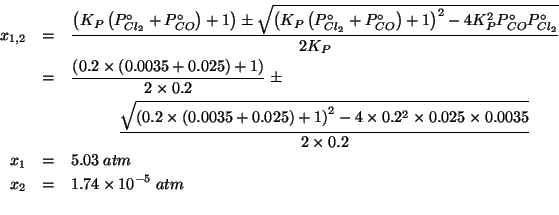
Chiaramente, la soluzione ![]() non e' accettabile poiche'
implicherebbe una violazione del principio di conservazione della
massa. L'unica soluzione accettabile rimane cosi'
non e' accettabile poiche'
implicherebbe una violazione del principio di conservazione della
massa. L'unica soluzione accettabile rimane cosi' ![]() .
.
Dati:

Altri simboli:
| massa di anidride carbonica in |
|
| massa di acqua in |
|
| massa di carbonio in |
|
| massa di idrogeno in |
|
| numero di moli di anidride carbonica | |
| numero di moli di acqua | |
| numero di moli di atomi di carbonio | |
| numero di moli di atomi di idrogeno | |
| massa molare dell'anidride carbonica: |
|
| massa molare dell'acqua: |
|
| massa molare del carbonio: |
|
| massa molare dell'idrogeno: |
Se indichiamo con ![]() la formula molecolare della sostanza,
la reazione di combustione puo' essere rappresentata con la seguente
equazione:
la formula molecolare della sostanza,
la reazione di combustione puo' essere rappresentata con la seguente
equazione:
Dalla stechiometria si vede che il numero di moli di anidride
carbonica prodotta e' uguale al numero di moli di carbonio presenti
in ![]() di sostanza. Analogamente, il numero di moli di acqua
prodotta e' uguale alla meta' del numero di moli di idrogeno presenti
nella stessa massa di sostanza.
di sostanza. Analogamente, il numero di moli di acqua
prodotta e' uguale alla meta' del numero di moli di idrogeno presenti
nella stessa massa di sostanza.
Allora:
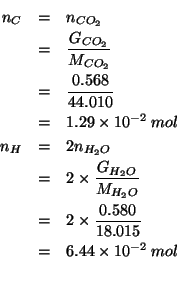
I numeri di moli trovati possono essere trasformati immediatamente nelle corrispondenti masse in grammi:
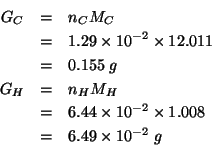
Ora non resta che trovare le percentuali in massa di ![]() e
e ![]() :
:
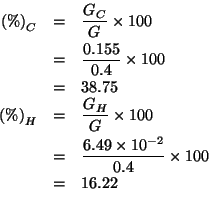
Ovviamente, la percentuale di azoto si trova per differenza: