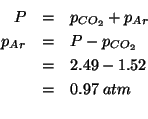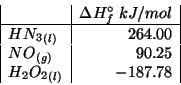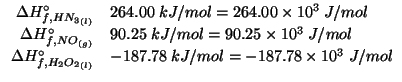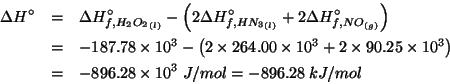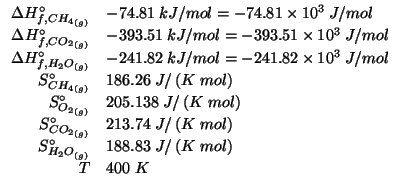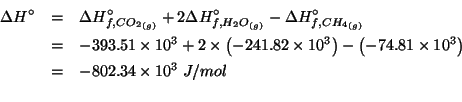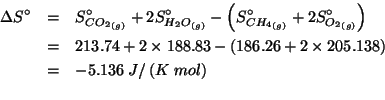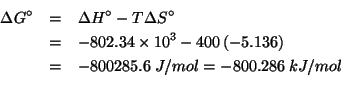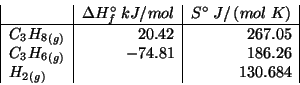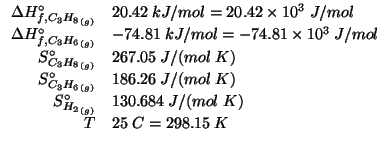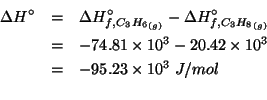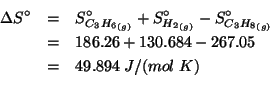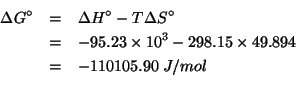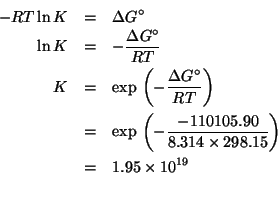Dati:
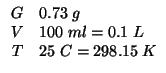
Altri simboli:
| massa molare di |
|
|
|
concentrazione molare formale del sale |
|
|
numero di moli del sale |
| costante dei gas:
|
La legge della pressione osmotica e':
La concentrazione che compare nella legge e' la concentrazione colligativa, cioe' la concentrazione di tutte le particelle cui da' origine il soluto in soluzione.
In questo caso il soluto e' un sale e, come tale, in soluzione e' completamente ionizzato secondo:
Per ogni mole di sale sciolto si generano in soluzione ![]() moli di
ioni (non importa la loro identita'). Quindi:
moli di
ioni (non importa la loro identita'). Quindi:
Per definizione di concentrazione molare:
Inoltre:
Sostituendo a ritroso:
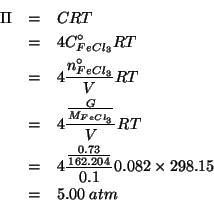
Dati:
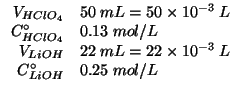
Altri simboli:
| numero di moli iniziale di ioni idronio | |
|
|
numero di moli iniziale di ioni ossidrile |
| prodotto ionico dell'acqua:
|
Sia l'acido che la base mescolati sono forti e quindi completamente dissociati. In pratica, dunque, la reazione che avviene in soluzione e' la reazione di neutralizzazione:
La costante di equilibrio di questa reazione e' l'inversa della
costante del prodotto ionico dell'acqua: essa vale quindi
![]() . Dato il valore grande della costante di equilibrio, la
reazione si puo' considerare completa. Allora si deve stabilire
qual'e' il reagente limitante.
. Dato il valore grande della costante di equilibrio, la
reazione si puo' considerare completa. Allora si deve stabilire
qual'e' il reagente limitante.
Valutiamo quindi il numero di moli di ioni idronio ed ossidrile, che, ovviamente, sono dati da:
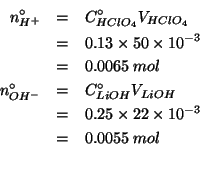
Si vede quindi che il reagente limitante e' lo ione ossidrile.
Allora:
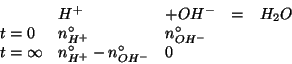
La concentrazione finale di ioni idronio si ottiene dividendo il numero di moli per il volume totale della soluzione:
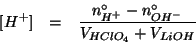
e infine:
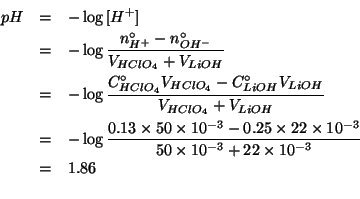
Dati:

L'espressione che fornisce il ![]() di un tampone e' stata ricavata
durante il corso:
di un tampone e' stata ricavata
durante il corso:
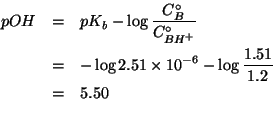
Infine:
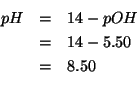
Dati:
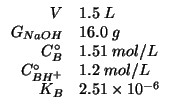
Altri simboli:
| massa molare di |
|
| numero di moli iniziale di |
|
|
|
numero di moli iniziale di |
|
|
numero di moli iniziale di |
Gli ioni ossidrile aggiunti (sotto forma di ![]() ) andranno a
reagire con l'acido
) andranno a
reagire con l'acido ![]() , secondo:
, secondo:
Questa reazione e' l'inversa della reazione di ionizzazione basica
della base debole ![]() e quindi la sua costante di equilibrio e'
l'inversa della costante
e quindi la sua costante di equilibrio e'
l'inversa della costante ![]() . SI tratta quindi di una costante di
equilibrio grande e pertanto la reazione si puo' considerare
completa. Dobbiamo allora trovare il reagente limitante:
. SI tratta quindi di una costante di
equilibrio grande e pertanto la reazione si puo' considerare
completa. Dobbiamo allora trovare il reagente limitante:
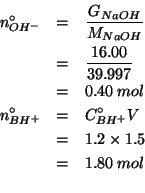
E' evidente che il reagente limitante e' lo ione ossidrile.
Allora:
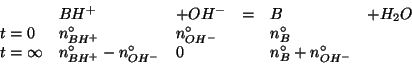
I numeri di moli della base debole e del suo acido coniugato dopo la
reazione con gli ioni ossidrile possono ora essere inseriti
nell'espressione che fornisce il ![]() del tampone:
del tampone:
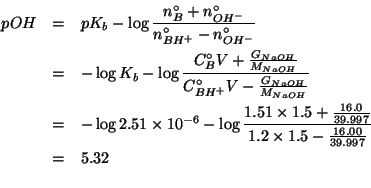
Infine:
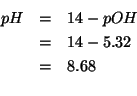
Applicando il metodo visto durante il corso si ha:
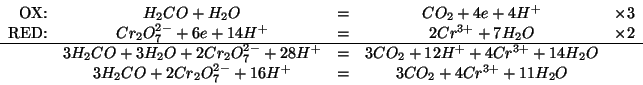
Dati:
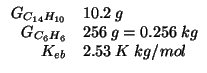
Altri simboli:
|
|
numero di moli di antracene |
|
|
massa molare dell'antracene:
|
| molalita' |
Usando la legge dell'innalzamento ebullioscopico:
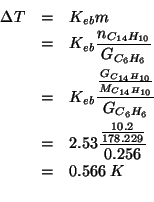
Secondo quanto spiegato durante il corso, cominciamo a scrivere una formula di Lewis corretta per la molecola in questione.
| Elettroni di valenza | |
| carica | |
| totale | |
Ponendo l'atomo di cloro (meno elettronegativo) al centro si ottiene:

Si puo' facilmente verificare che questa e' la formula di risonanza piu' stabile. Tuttavia, la particolare formula di risonanza che si considera (purche' corretta!) non ha importanza, poiche' siamo interessati alla geometria molecolare, che non dipende dalla particolare formula di risonanza considerata.
Dalla formula di Lewis si ricava subito che il numero di coppie
strutturali e' ![]() . Da cio' segue che la geometria delle coppie
strutturali e' bipiramidale trigonale.
. Da cio' segue che la geometria delle coppie
strutturali e' bipiramidale trigonale.
Le due coppie di non legame si disporranno in posizioni equatoriali (meno ingombrate rispetto a quelle assiali): ne segue che la geometria molecolare sara' a ``T''.
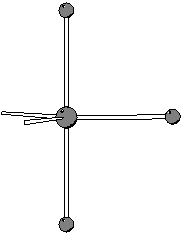 |
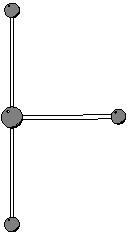 |
| geometria delle coppie strutturali | geometria molecolare |
Dati:
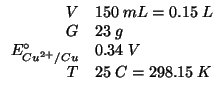
Altri simboli:
|
|
massa molare di
|
|
|
numero di moli di
|
| numero di moli di |
|
| costante di Faraday: |
|
| costante dei gas:
|
Il potenziale elettrodico in condizioni non standard e' dato dalla
equazione di Nernst. Per la coppia ![]() si ha:
si ha:
e quindi:
Per la definizione di concentrazione molare:
Quindi:
Il numero di moli di ioni ![]() in soluzione e' in relazione con
il numero di moli di
in soluzione e' in relazione con
il numero di moli di
![]() , tramite la
stechiometria della reazione di ionizzazione del sale (completa, come
per tutti i sali):
, tramite la
stechiometria della reazione di ionizzazione del sale (completa, come
per tutti i sali):
E' chiaro che:
e quindi:
Il numero di moli di
![]() si ricava facilmente
dalla massa in grammi e dalla massa molare:
si ricava facilmente
dalla massa in grammi e dalla massa molare:
In definitiva:
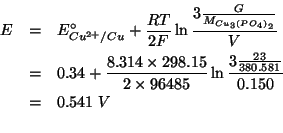
Altri simboli:
|
|
massa molare di
|
| massa molare di |
|
| massa molare di |
|
| massa molare di |
|
| numero di moli di |
|
| numero di moli di |
|
| numero di moli di |
|
| massa di |
|
| massa di |
|
| massa di |
La composizione percentuale di un composto e' ovviamente indipendente
dalla massa di composto considerata. Allora, per comodita',
consideriamo una massa di
![]() pari alla sua
massa molare. E' chiaro che tale massa di composto conterra':
pari alla sua
massa molare. E' chiaro che tale massa di composto conterra':
Questi numeri di moli possono essere trasformati facilmente nelle corrispondenti masse:
Queste masse sono le masse dei tre elementi costituenti il composto contenute in una massa molare del composto. Quindi la composizione percentuale e':
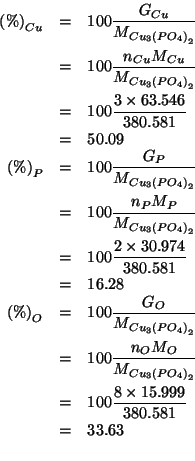
Dati:
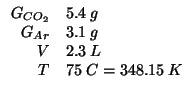
Altri simboli:
| massa molare di |
|
| massa molare di |
|
| numero di moli di |
|
| numero di moli di |
|
| numero totale di moli | |
| pressione totale in |
|
| pressione parziale di |
|
| pressione parziale di |
|
| costante dei gas:
|
Per la pressione totale, dalla legge dei gas ideali:
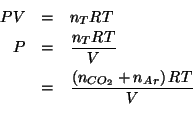
I numeri di moli dei due componenti si esprimono in funzione delle relative masse e masse molari:
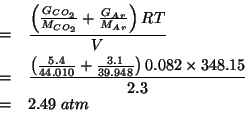
La pressione parziale di ![]() si trova direttamente dalla sua
definizione:
si trova direttamente dalla sua
definizione:
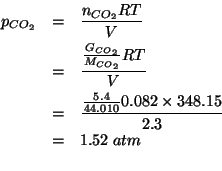
Infine, la pressione parziale di ![]() si ottiene per differenza,
visto che:
si ottiene per differenza,
visto che: