67.
In questa sezione vogliamo dimostrare che, detti ![]() ,
,
![]() e
e ![]() rispettivamente il grado di dissociazione, la
costante di dissociazione e la concentrazione iniziale di un
elettrolita debole, si ha:
rispettivamente il grado di dissociazione, la
costante di dissociazione e la concentrazione iniziale di un
elettrolita debole, si ha:
Consideriamo l'equilibrio di dissociazione per l'elettrolita debole
![]() e scriviamo le concentrazioni di equilibrio in funzione del
grado di dissociazione:
e scriviamo le concentrazioni di equilibrio in funzione del
grado di dissociazione:
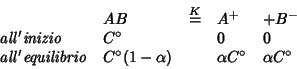
La legge dell'azione di massa per l'equilibrio su scritto recita:
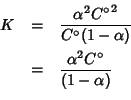
Generalmente, a questo punto, se ![]() e' abbastanza grande e
e' abbastanza grande e
![]() e' abbastanza piccola, si puo' assumere che la frazione di
elettrolita dissociato (
e' abbastanza piccola, si puo' assumere che la frazione di
elettrolita dissociato (![]() ) sia trascurabile rispetto a
) sia trascurabile rispetto a ![]() e quindi si ottiene il risultato valido a concentrazioni finite
che abbiamo visto a pagina
e quindi si ottiene il risultato valido a concentrazioni finite
che abbiamo visto a pagina ![]() :
:
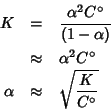
Se pero' supponiamo che
![]() , questa
approssimazione non e' piu' lecita. Allora, riarrangiando la legge
dell'azione di massa si ottiene:
, questa
approssimazione non e' piu' lecita. Allora, riarrangiando la legge
dell'azione di massa si ottiene:
da cui, scartando ovviamente la soluzione con il segno meno davanti al radicale, si ottiene:
Per dimostrare la tesi, osserviamo che il termine sotto radice quadrata si puo' riscrivere come:
e quindi:
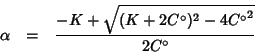
Ora, se
![]() , nel radicale il termine
, nel radicale il termine
![]() diventa trascurabile rispetto al termine
diventa trascurabile rispetto al termine
![]() e quindi
e quindi
![]() .
Di conseguenza, per
.
Di conseguenza, per ![]() si ha:
si ha:
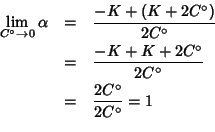
che e' cio' che volevamo dimostrare.