


Next: 19990617: different randomization wrt
Up: MD work on
Previous: 19990602: Same input on
19990614: lattice constant from GULP, but NO thermal
expansion
It looks like the lattice constant influences very heavily the
quality of the MSD plots obtained from a given simulation (compare
19981124 and 19981126). The lattice constant used in 19981126 (which was the
same used in 19981113-19981117-19981119), which gives a good MSD plot, was
taken from the paper of Brinkman [2], which deals with
YSZ (and not ceria-zirconia). I'd like to find an acceptable method
for selecting the lattice constant for the simulations. It seems that
taking thermal expansion into account yelds lattice constants too
large (see 19981124). So a new attempt: take GULP optimized
lattice constant without correction for thermal expansion. By
the way the lattice constants obtained from GULP agree very well
with values obtainable from the Vegard law.
The system to be simulated is:
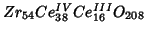 . This corresponds to the
following occupancies:
. This corresponds to the
following occupancies:
I run GULP with the above occupancies, polarizable oxygen and rigid
cations (same conditions as the DL_POLY run) and get the follwoing
value for the optimized lattice constant:
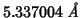 .
.
The lattice constant of the fluorite structure is related to the sum
of the cationic (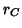 ) and anionic (
) and anionic (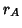 ) radii by the following
relation:
) radii by the following
relation:
(the above follows immediately from the fact that the oxygen ion is at
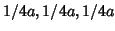 , i.e. along the diagonal of the cubic unit
cell. Thus, assuming that the cation and the anion are in contact, one
can say:
, i.e. along the diagonal of the cubic unit
cell. Thus, assuming that the cation and the anion are in contact, one
can say:
)
According to Vegard's law (see for instance p.367 of
reference [4]), the cationic radius for the
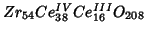 system should be an
average of the values for the three cation components:
system should be an
average of the values for the three cation components:
This can be substituted in the expression for the lattice constant
above, taking the following values for the ionic radii [5]:
The value so obtained is:
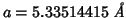 , in close
agreement with GULP.
, in close
agreement with GULP.
(In the Vegard's law calculation I've not considered the
fractional occupancy of the oxygen sites: I think this should be more
or less correct)
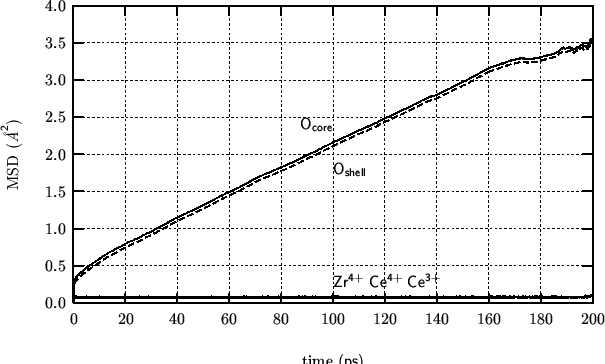
Got rather nice MSD's. Have to keep this as a starting point for
future developments.
why are the MSD's for oxygen cores and oxygen
shells shifted?
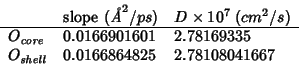
From the slope of the oxygen MSD's I get the following diffusion
coefficient, using the relation:
(MSD data fitted in the interval
![$[20.0:160.0]\;ps$](img99.gif) )
)
The diffusion coefficients for
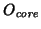 and
and
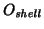 are identical and match quite well that in 19981127.
are identical and match quite well that in 19981127.



Next: 19990617: different randomization wrt
Up: MD work on
Previous: 19990602: Same input on
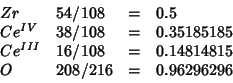
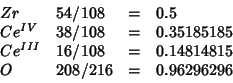
![]() .
.
![]() , i.e. along the diagonal of the cubic unit
cell. Thus, assuming that the cation and the anion are in contact, one
can say:
, i.e. along the diagonal of the cubic unit
cell. Thus, assuming that the cation and the anion are in contact, one
can say:
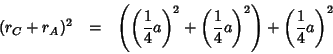
![]() system should be an
average of the values for the three cation components:
system should be an
average of the values for the three cation components:

![]() , in close
agreement with GULP.
, in close
agreement with GULP.
![]() )
)
![]() and
and
![]() are identical and match quite well that in 19981127.
are identical and match quite well that in 19981127.