42.
Per un qualsiasi conduttore (sia esso un metallo o una
soluzione elettrolitica), la conducibilita' o
conduttanza (simbolo ![]() ) e' definita come l'inverso
della sua resistenza
) e' definita come l'inverso
della sua resistenza ![]() :
:
Il significato fisico di questa grandezza e' chiaro: la conducibilita' di un conduttore e' una misura della sua capacita' di farsi attraversare da una corrente elettrica.
L'unita' di misura della conducibilita' e' il Siemens (simbolo ![]() ):
dalla definizione su scritta si deduce che
):
dalla definizione su scritta si deduce che
![]() .
.
La resistenza di un conduttore dipende sia dalla sua natura (cioe' se
si tratta di rame o alluminio o di una soluzione di ![]() ) che
dalle sue caratteristiche geometriche, cioe' in ultima analisi, dalla
sua forma e dimensione. Questa duplice dipendenza puo' essere espressa
in forma esplicita; se indichiamo con
) che
dalle sue caratteristiche geometriche, cioe' in ultima analisi, dalla
sua forma e dimensione. Questa duplice dipendenza puo' essere espressa
in forma esplicita; se indichiamo con ![]() la sezione e con
la sezione e con ![]() la
lunghezza di un conduttore, allora la sua resistenza
la
lunghezza di un conduttore, allora la sua resistenza ![]() e'
esprimibile con:
e'
esprimibile con:
In questa relazione, il termine ![]() tiene conto della geometria,
mentre il termine
tiene conto della geometria,
mentre il termine ![]() dipende solo dalla natura del
conduttore e si chiama resistenza specifica o
resistivita'.
dipende solo dalla natura del
conduttore e si chiama resistenza specifica o
resistivita'.
Se sostituiamo l'espressione per ![]() nella definizione di
nella definizione di
![]() otteniamo:
otteniamo:
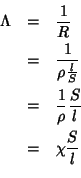
dove abbiamo posto ![]() . In analogia con quanto detto per
la resistenza, questa relazione mette in evidenza che la
conducibilita' di un conduttore dipende dalla sua natura (
. In analogia con quanto detto per
la resistenza, questa relazione mette in evidenza che la
conducibilita' di un conduttore dipende dalla sua natura (![]() ) e
dalla sua geometria (
) e
dalla sua geometria (![]() ).
). ![]() viene detta conducibilita'
specifica e, come
viene detta conducibilita'
specifica e, come ![]() , dipende solo dalla natura del
conduttore. Le dimensioni di
, dipende solo dalla natura del
conduttore. Le dimensioni di ![]() si deducono dall'espressione
appena scritta: se
si deducono dall'espressione
appena scritta: se ![]() e' espressa in
e' espressa in ![]() e
e ![]() in
in ![]() ,
allora
,
allora ![]() risulta espressa in
risulta espressa in ![]() .
.
Nel caso in cui il conduttore sia una soluzione elettrolitica, la sua conducibilita' si misura con una cella conduttimetrica (figura 2.1).
In pratica, una porzione di soluzione viene confinata tra due elettrodi (generalmente di platino). Uno strumento ( conduttimetro) fa circolare una corrente alternata di elevata frequenza fra gli elettrodi e misura la resistenza della soluzione compresa fra essi. L'inverso di tale resistenza e' naturalmente la conducibilita' cercata.
L'impiego della corrente alternata invece che continua e' essenziale. Invertendo rapidamente e continuamente la polarita' degli elettrodi si impediscono infatti fenomeni di elettrolisi che cambierebbero la concentrazione delle specie ioniche in soluzione.
43.
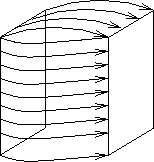
Mentre la definizione della
geometria di un conduttore metallico e' semplice, le dimensioni del
conduttore elettrolitico compreso fra gli elettrodi di una cella
conduttimetrica non coincidono esattamente con il parallelepipedo
ideale definito dagli elettrodi: infatti, la corrente circola anche
nella soluzione che sta al di fuori di tale parallelepipedo
(figura 2.2). Cio' fa si' che il rapporto ![]() che compare nell'espressione di
che compare nell'espressione di ![]() su scritta venga
generalmente indicato con
su scritta venga
generalmente indicato con ![]() e chiamato costante di cella:
e chiamato costante di cella:
|
Anche se ![]() e' difficile da determinare sulla base della geometria
``apparente'' degli elettrodi, tuttavia, una volta fissata la cella
conduttimetrica, esso rimane sicuramente costante e puo' quindi essere
determinato una volta per tutte misurando la conducibilita' di una
soluzione avente conducibilita' specifica nota:
e' difficile da determinare sulla base della geometria
``apparente'' degli elettrodi, tuttavia, una volta fissata la cella
conduttimetrica, esso rimane sicuramente costante e puo' quindi essere
determinato una volta per tutte misurando la conducibilita' di una
soluzione avente conducibilita' specifica nota:
A questo scopo si usano generalmente soluzioni di ![]() , la cui
conducibilita' specifica e' nota con grande accuratezza per diversi
valori di concentrazione e temperatura.
, la cui
conducibilita' specifica e' nota con grande accuratezza per diversi
valori di concentrazione e temperatura.
La relazione
![]() ci dice che la conducibilita' di una
soluzione dipende dalla geometria della cella impiegata per la sua
misura (
ci dice che la conducibilita' di una
soluzione dipende dalla geometria della cella impiegata per la sua
misura (![]() ) e da un parametro ``intrinseco'' (
) e da un parametro ``intrinseco'' (![]() ), indipendente
da fattori strumentali e dipendente unicamente dalla natura della
soluzione. Come vedremo,
), indipendente
da fattori strumentali e dipendente unicamente dalla natura della
soluzione. Come vedremo, ![]() e' in relazione con la
concentrazione delle specie ioniche presenti in soluzione e cio'
rappresenta la base per le applicazioni analitiche della
conduttimetria.
e' in relazione con la
concentrazione delle specie ioniche presenti in soluzione e cio'
rappresenta la base per le applicazioni analitiche della
conduttimetria.