13.
Consideriamo un elettrodo ad ![]() , il
cui potenziale elettrodico di equilibrio e' dato da:
, il
cui potenziale elettrodico di equilibrio e' dato da:
![\begin{eqnarray*}
E&=&E^{\circ}_{Ag^+/Ag}-\frac{RT}{F}\ln\left[Ag^+\right]\\
\end{eqnarray*}](img88.gif)
Questa espressione puo' essere facilmente posta nella forma:
il che suggerirebbe un impiego immediato di questo elettrodo per la
determinazione della concentrazione di ioni ![]() in una soluzione:
immergiamo nella soluzione da analizzare un filo di
in una soluzione:
immergiamo nella soluzione da analizzare un filo di ![]() , misuriamo
, misuriamo
![]() e
e ![]() , i valori di
, i valori di
![]() ,
, ![]() e
e ![]() sono
tabulati e quindi ricaviamo la concentrazione incognita di ioni
argento.
sono
tabulati e quindi ricaviamo la concentrazione incognita di ioni
argento.
Purtroppo, la semplice procedura descritta non e' possibile perche' la misura diretta del potenziale elettrodico di un singolo elettrodo non e' sperimentalmente accessibile.
Esistono argomenti rigorosi che dimostrano quanto detto, ma questi vanno oltre il livello a cui vogliamo mantenerci. Tuttavia, possiamo convincerci ugualmente bene dell'impossibilita' di misurare un singolo potenziale elettrodico immaginando un semplice esperimento.
14.
Una differenza di
potenziale elettrico si misura con uno strumento detto
voltmetro (o potenziometro). Esso e' costituito da una
``scatola nera'' (il cui funzionamento non ci interessa) da cui escono
due cavi che terminano con dei puntali metallici contrassegnati
generalmente con i simboli ![]() e
e ![]() (generalmente, il
cavo del puntale
(generalmente, il
cavo del puntale ![]() e' di colore rosso, mentre quello del
puntale
e' di colore rosso, mentre quello del
puntale ![]() e' di colore nero). Ponendo in contatto i puntali
con due punti di un circuito elettrico, lo strumento fornisce la
differenza di potenziale fra i due punti. Tale differenza e' letta
dallo strumento come:
e' di colore nero). Ponendo in contatto i puntali
con due punti di un circuito elettrico, lo strumento fornisce la
differenza di potenziale fra i due punti. Tale differenza e' letta
dallo strumento come:
(quindi, scambiando i due puntali, si ottiene lo stesso valore della differenza di potenziale, ma cambiato di segno)
Immaginiamo allora di voler misurare il potenziale elettrodico di una
semicella ad ![]() con un voltmetro
(figura 1.3). Ricordiamo che, per definizione, il
potenziale elettrodico di questa semicella e' la differenza di
potenziale fra il filo di argento e la soluzione. Quindi, per misurare
questa differenza di potenziale con il voltmetro, dovremmo toccare il
filo metallico con il puntale
con un voltmetro
(figura 1.3). Ricordiamo che, per definizione, il
potenziale elettrodico di questa semicella e' la differenza di
potenziale fra il filo di argento e la soluzione. Quindi, per misurare
questa differenza di potenziale con il voltmetro, dovremmo toccare il
filo metallico con il puntale ![]() e la soluzione con
quello
e la soluzione con
quello ![]() .
.
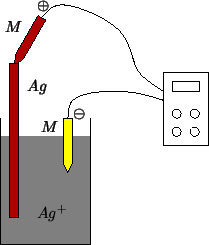
|
Ma, quando immergiamo il puntale ![]() del voltmetro nella
soluzione, si realizza inevitabilmente una seconda semicella, in cui
la parte metallica (il conduttore elettronico) e' il puntale del
voltmetro e la soluzione e' la stessa della semicella
del voltmetro nella
soluzione, si realizza inevitabilmente una seconda semicella, in cui
la parte metallica (il conduttore elettronico) e' il puntale del
voltmetro e la soluzione e' la stessa della semicella ![]() . Ne
segue che il voltmetro non misurera' il potenziale elettrodico della
semicella
. Ne
segue che il voltmetro non misurera' il potenziale elettrodico della
semicella ![]() , ma quello della cella elettrochimica
costituita dall'accoppiamento della semicella
, ma quello della cella elettrochimica
costituita dall'accoppiamento della semicella ![]() con la
semicella ottenuta all'atto dell'immersione del puntale
con la
semicella ottenuta all'atto dell'immersione del puntale ![]() del voltmetro nella soluzione.
del voltmetro nella soluzione.
E' importante comprendere bene che cosa misura il voltmetro in questo esperimento. A tale scopo dobbiamo conoscere alcune semplici proprieta' del potenziale elettrico. La prima e' che il potenziale elettrico in tutti i punti di un conduttore metallico o di una soluzione si puo' considerare con buona approssimazione costante; la seconda e' che la differenza di potenziale fra due punti di un qualsiasi circuito elettrico e' sempre esprimibile come somma algebrica delle differenze di potenziale ``parziali'' incontrate lungo il percorso fra i due punti in questione (una differenza di potenziale e' come il dislivello totale di una montagna, che puo' essere espresso come somma algebrica di tutti i dislivelli parziali che si incontrano lungo il percorso per raggiungere la vetta).
Il puntale ![]() del voltmetro in contatto con il filo
di argento rappresenta un unico conduttore metallico il cui
potenziale elettrico avra' lo stesso valore in tutti i punti (diciamo
che il volume di questo conduttore e' equipotenziale):
chiamiamo
del voltmetro in contatto con il filo
di argento rappresenta un unico conduttore metallico il cui
potenziale elettrico avra' lo stesso valore in tutti i punti (diciamo
che il volume di questo conduttore e' equipotenziale):
chiamiamo ![]() tale potenziale elettrico; il puntale
tale potenziale elettrico; il puntale ![]() del voltmetro costituisce un secondo conduttore metallico
equipotenziale: indichiamo con
del voltmetro costituisce un secondo conduttore metallico
equipotenziale: indichiamo con ![]() il valore del suo potenziale
(
il valore del suo potenziale
(![]() sta ad indicare il metallo di cui e' fatto il puntale);
chiaramente,
sta ad indicare il metallo di cui e' fatto il puntale);
chiaramente, ![]() ed
ed ![]() sono diversi e il display del
voltmetro fornisce proprio la loro differenza:
sono diversi e il display del
voltmetro fornisce proprio la loro differenza: ![]() . Il
significato di questa differenza si puo' comprendere se la decomponiamo
nei contributi parziali che si incontrano andando dal puntale
. Il
significato di questa differenza si puo' comprendere se la decomponiamo
nei contributi parziali che si incontrano andando dal puntale
![]() al puntale
al puntale ![]() . Con riferimento alla
figura 1.3, se partiamo dal puntale
. Con riferimento alla
figura 1.3, se partiamo dal puntale ![]() e ci
muoviamo all'interno di esso o del filo di argento, il potenziale e'
sempre lo stesso; quando passiamo dal filo di argento alla soluzione,
incontriamo una prima differenza di potenziale: indicando con
e ci
muoviamo all'interno di esso o del filo di argento, il potenziale e'
sempre lo stesso; quando passiamo dal filo di argento alla soluzione,
incontriamo una prima differenza di potenziale: indicando con ![]() il potenziale (comune a tutti i punti) della soluzione, questa prima
differenza di potenziale e'
il potenziale (comune a tutti i punti) della soluzione, questa prima
differenza di potenziale e'
![]() . Una volta
nella soluzione, il potenziale rimane costante finche' passiamo nel
puntale
. Una volta
nella soluzione, il potenziale rimane costante finche' passiamo nel
puntale ![]() : in questo passaggio registreremo una differenza
di potenziale data da
: in questo passaggio registreremo una differenza
di potenziale data da
![]() . Il puntale
. Il puntale
![]() e' equipotenziale e quindi non ci sono altri contributi
alla differenza di potenziale totale che il voltmetro misura.
e' equipotenziale e quindi non ci sono altri contributi
alla differenza di potenziale totale che il voltmetro misura.
In sostanza, indicando con ![]() la differenza di
potenziale totale misurata dal voltmetro, si ha (in base alla seconda
proprieta' del potenziale elettrico prima accennata):
la differenza di
potenziale totale misurata dal voltmetro, si ha (in base alla seconda
proprieta' del potenziale elettrico prima accennata):
![\begin{eqnarray*}
\mathit{ddp}&=&\Delta{}E_1+\Delta{}E_2\\
&=&E(Ag)-E(S)+E(S)-E(M)\\
&=&E(Ag)-E(S)-[E(M)-E(S)]\\
\end{eqnarray*}](img102.gif)
Vediamo quindi che il voltmetro misura la differenza fra i due termini
![]() e
e ![]() . In base alla definizione che
abbiamo dato di potenziale
elettrodico (punto 4), riconosciamo nel termine
. In base alla definizione che
abbiamo dato di potenziale
elettrodico (punto 4), riconosciamo nel termine
![]() il potenziale elettrodico del sistema
il potenziale elettrodico del sistema ![]() ;
analogamente, il termine
;
analogamente, il termine ![]() rappresenta il potenziale
elettrodico dell'elettrodo costituito dal metallo
rappresenta il potenziale
elettrodico dell'elettrodo costituito dal metallo ![]() immerso in una
soluzione contenente ioni
immerso in una
soluzione contenente ioni ![]() (non e' banale, ne' importante ai
fini della discussione, sapere qual'e' la reazione elettrodica che
caratterizza questo secondo elettrodo). Se indichiamo questi due
potenziali elettrodici con la notazione usuale
(non e' banale, ne' importante ai
fini della discussione, sapere qual'e' la reazione elettrodica che
caratterizza questo secondo elettrodo). Se indichiamo questi due
potenziali elettrodici con la notazione usuale ![]() e
e
![]() , otteniamo:
, otteniamo:
Questo risultato e' molto importante perche' ci mostra che, mentre un singolo potenziale elettrodico non si puo' misurare, e' possibile misurare la differenza fra due potenziali elettrodici di due semicelle accoppiate a formare una cella elettrochimica.
15.
In generale, una cella elettrochimica e' costituita da due
semicelle, ciascuna caratterizzata da una coppia redox ben definita
(figura 1.4). Ad esempio, potremmo accoppiare una semicella
ad ![]() con una semicella a
con una semicella a
![]() , oppure un
elettrodo a
, oppure un
elettrodo a ![]() con uno a
con uno a ![]() . In ogni caso, la
differenza di potenziale che si misura con un voltmetro toccando con i
puntali i due metalli delle semicelle e' uguale (a meno di una piccola
complicazione che tratteremo fra breve) alla differenza fra i due
potenziali elettrodici (potenziale elettrodico della semicella in
contatto col puntale
. In ogni caso, la
differenza di potenziale che si misura con un voltmetro toccando con i
puntali i due metalli delle semicelle e' uguale (a meno di una piccola
complicazione che tratteremo fra breve) alla differenza fra i due
potenziali elettrodici (potenziale elettrodico della semicella in
contatto col puntale ![]() meno potenziale elettrodico
della semicella in contatto col puntale
meno potenziale elettrodico
della semicella in contatto col puntale ![]() ).
).
Se indichiamo con
![]() il potenziale
elettrodico della semicella collegata al puntale
il potenziale
elettrodico della semicella collegata al puntale ![]() del
voltmetro (e caratterizzata dalla coppia redox
del
voltmetro (e caratterizzata dalla coppia redox
![]() ) e con
) e con
![]() quello della seconda semicella
(in cui reagisce la coppia redox
quello della seconda semicella
(in cui reagisce la coppia redox
![]() )
(figura 1.4), allora si ha:
)
(figura 1.4), allora si ha:
16.
Siccome un singolo potenziale elettrodico non e' misurabile,
si e' convenuto di assegnare arbitrariamente il valore di ![]() al potenziale standard di una semicella di riferimento e di esprimere
poi il potenziale di qualsiasi altro elettrodo relativamente al
riferimento. La semicella al cui potenziale standard e' stato
assegnato il valore nullo e' l'elettrodo standard a idrogeno (SHE:
Standard Hydrogen Electrode). Abbiamo gia' visto come e' costituito un
elettrodo a idrogeno (punto 12): nell'elettrodo
standard a idrogeno la concentrazione di ioni idrogeno nella soluzione
e la pressione parziale di idrogeno su di essa sono unitarie. In tal
modo, dall'equazione di Nernst, il potenziale elettrodico di questa
semicella coincide con il suo potenziale standard
(punto 11). Il fatto essenziale, al di la' del valore numerico
assegnato al potenziale dell'SHE, e' che esso e' costante (una
volta fissata la concentrazione degli ioni idrogeno e la pressione
parziale dell'idrogeno gassoso sopra la soluzione). Per assegnare il
potenziale a qualsiasi altro elettrodo relativamente all'SHE, si
costruisce una cella in cui l'elettrodo in questione viene accoppiato
con un SHE (figura 1.5): con un voltmetro si misura la
differenza di potenziale fra l'elettrodo di cui si vuole conoscere il
potenziale relativo e il filo di
al potenziale standard di una semicella di riferimento e di esprimere
poi il potenziale di qualsiasi altro elettrodo relativamente al
riferimento. La semicella al cui potenziale standard e' stato
assegnato il valore nullo e' l'elettrodo standard a idrogeno (SHE:
Standard Hydrogen Electrode). Abbiamo gia' visto come e' costituito un
elettrodo a idrogeno (punto 12): nell'elettrodo
standard a idrogeno la concentrazione di ioni idrogeno nella soluzione
e la pressione parziale di idrogeno su di essa sono unitarie. In tal
modo, dall'equazione di Nernst, il potenziale elettrodico di questa
semicella coincide con il suo potenziale standard
(punto 11). Il fatto essenziale, al di la' del valore numerico
assegnato al potenziale dell'SHE, e' che esso e' costante (una
volta fissata la concentrazione degli ioni idrogeno e la pressione
parziale dell'idrogeno gassoso sopra la soluzione). Per assegnare il
potenziale a qualsiasi altro elettrodo relativamente all'SHE, si
costruisce una cella in cui l'elettrodo in questione viene accoppiato
con un SHE (figura 1.5): con un voltmetro si misura la
differenza di potenziale fra l'elettrodo di cui si vuole conoscere il
potenziale relativo e il filo di ![]() dell'SHE; come abbiamo appena
visto, la differenza di potenziale misurata e':
dell'SHE; come abbiamo appena
visto, la differenza di potenziale misurata e':
Avendo posto
![]() , segue che la differenza di
potenziale misurata dal voltmetro coincide con il potenziale
elettrodico relativo della semicella considerata (l'aggettivo
relativo significa quindi che questo valore dipende dal fatto
che abbiamo scelto di assegnare il valore
, segue che la differenza di
potenziale misurata dal voltmetro coincide con il potenziale
elettrodico relativo della semicella considerata (l'aggettivo
relativo significa quindi che questo valore dipende dal fatto
che abbiamo scelto di assegnare il valore ![]() all'SHE, ovvero,
identicamente, che viene espresso come differenza fra il
potenziale elettrodico ``assoluto'' della semicella e il
potenziale elettrodico ``assoluto'' dell'SHE). Chiaramente,
se nella semicella accoppiata con l'SHE la concentrazione di tutte le
specie partecipanti alla semireazione redox e' unitaria, la differenza
di potenziale misurata con il voltmetro coincide con il potenziale
standard relativo della semicella.
all'SHE, ovvero,
identicamente, che viene espresso come differenza fra il
potenziale elettrodico ``assoluto'' della semicella e il
potenziale elettrodico ``assoluto'' dell'SHE). Chiaramente,
se nella semicella accoppiata con l'SHE la concentrazione di tutte le
specie partecipanti alla semireazione redox e' unitaria, la differenza
di potenziale misurata con il voltmetro coincide con il potenziale
standard relativo della semicella.
17.
Il fatto di poter definire solo potenziali elettrodici
relativi non rappresenta un problema. Infatti, in primo luogo, la
differenza fra due potenziali elettrodici relativi e' uguale alla
differenza fra i loro valori ``assoluti''. Cio' segue immediatamente
dalla definizione di potenziale relativo che abbiamo dato: se
indichiamo con
![]() e
e
![]() i potenziali elettrodici
``assoluti'' di due coppie redox qualsiasi, allora si ha:
i potenziali elettrodici
``assoluti'' di due coppie redox qualsiasi, allora si ha:
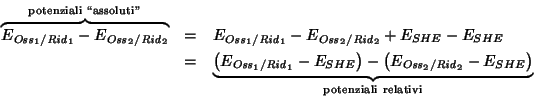
Inoltre l'equazione di Nernst mantiene inalterata la sua forma se
invece del potenziale ``assoluto'' si usa quello relativo. Se
indichiamo con l'indice ![]() i valori ``assoluti'' e con
l'indice
i valori ``assoluti'' e con
l'indice ![]() quelli relativi, allora, prendendo l'esempio
della coppia
quelli relativi, allora, prendendo l'esempio
della coppia
![]() , si ha:
, si ha:
![\begin{eqnarray*}
E_{\mathit{ass}}&=&E^\circ_{Fe^{3+}/Fe^{2+},\mathit{ass}}+\fra...
...ac{RT}{F}\ln\frac{\left[Fe^{3+}\right]}{\left[Fe^{2+}\right]}\\
\end{eqnarray*}](img121.gif)
Apparentemente, quindi, il potenziale elettrodico che compare nella legge di Nernst puo' essere pensato indifferentemente come relativo (definito rispetto all'SHE) o ``assoluto'' (non misurabile).
18.
La scelta dell'SHE come elettrodo di riferimento, pur essendo
quella internazionalmente riconosciuta, non e' sicuramente l'unica
possibile ne' la piu' conveniente: qualsiasi semicella il cui
potenziale elettrodico sia costante e riproducibile puo' servire da
riferimento. Naturalmente, il valore numerico di un potenziale
relativo cambia al variare dell'elettrodo di riferimento: tuttavia, e'
sempre possibile convertire un potenziale elettrodico misurato
rispetto ad un riferimento diverso dall'SHE nel corrispondente valore
rispetto all'SHE. Infatti, se indichiamo con ![]() il potenziale
``assoluto'' di una data semicella, con
il potenziale
``assoluto'' di una data semicella, con
![]() il
potenziale ``assoluto'' di una semicella di riferimento (diversa
dall'SHE) e con
il
potenziale ``assoluto'' di una semicella di riferimento (diversa
dall'SHE) e con
![]() il potenziale ``assoluto''
dell'SHE, allora si puo' scrivere:
il potenziale ``assoluto''
dell'SHE, allora si puo' scrivere:
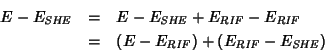
il che mostra che il potenziale di una semicella riferito all'SHE
![]() si ottiene sommando il suo
potenziale riferito a un qualsiasi altro riferimento
si ottiene sommando il suo
potenziale riferito a un qualsiasi altro riferimento
![]() al potenziale relativo all'SHE
della semicella usata come riferimento
al potenziale relativo all'SHE
della semicella usata come riferimento
![]() .
.
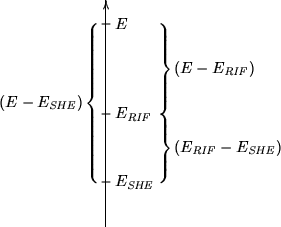
Questo risultato e' espresso graficamente nella
figura 1.6, dove, sull'asse dei potenziali
``assoluti'', sono indicati ![]() ,
,
![]() ed
ed
![]() e viene mostrata la relazione fra essi.
e viene mostrata la relazione fra essi.
 |
19.
Nel concetto di potenziale relativo che
abbiamo introdotto non c'e' nulla di ``esoterico''. Potremmo definire
in modo assolutamente identico una statura relativa in una classe di
studenti. Prendiamo uno studente di riferimento e definiamo la statura
relativa di uno studente qualsiasi come la differenza fra la sua
statura ``assoluta'' e quella dello studente di riferimento. In tal
modo, se uno studente ha una statura relativa di ![]() cio'
significa semplicemente che egli e' piu' alto dello studente di
riferimento di
cio'
significa semplicemente che egli e' piu' alto dello studente di
riferimento di ![]() ; analogamente, uno studente che abbia una
statura relativa di
; analogamente, uno studente che abbia una
statura relativa di ![]() sara' piu' basso dello studente di
riferimento di
sara' piu' basso dello studente di
riferimento di ![]() . Appare evidente che definire la statura
relativa in questo modo e' equivalente ad assegnare allo
studente di riferimento una statura nulla (esattamente come abbiamo
fatto per il potenziale dell'SHE). E' chiaro inoltre che la statura
relativa di uno studente sara' diversa per diverse scelte dello
studente di riferimento. Infine, e' sempre possibile convertire una
statura relativa riferita ad un certo studente nella statura relativa
riferita ad uno studente diverso: se la statura relativa di Marco
rispetto a Ottavia e'
. Appare evidente che definire la statura
relativa in questo modo e' equivalente ad assegnare allo
studente di riferimento una statura nulla (esattamente come abbiamo
fatto per il potenziale dell'SHE). E' chiaro inoltre che la statura
relativa di uno studente sara' diversa per diverse scelte dello
studente di riferimento. Infine, e' sempre possibile convertire una
statura relativa riferita ad un certo studente nella statura relativa
riferita ad uno studente diverso: se la statura relativa di Marco
rispetto a Ottavia e' ![]() e la statura relativa di Ottavia
rispetto ad Andrea e'
e la statura relativa di Ottavia
rispetto ad Andrea e' ![]() , allora la statura relativa di Marco
rispetto al ``riferimento'' Andrea sara'
, allora la statura relativa di Marco
rispetto al ``riferimento'' Andrea sara' ![]() (vi appare chiaro il parallelo con la figura 1.6?)
(vi appare chiaro il parallelo con la figura 1.6?)
20.
L'elettrodo standard a idrogeno non
e' molto comodo da usare in pratica. Per questo motivo, vengono usati
come riferimenti altri elettrodi piu' semplici da costruire e
utilizzare. Due elettrodi di riferimento molto usati sono l'elettrodo
ad ![]() e quello a calomelano, che abbiamo gia' visto al
punto 3. Essi sono schematicamente illustrati
nella figura 1.7.
e quello a calomelano, che abbiamo gia' visto al
punto 3. Essi sono schematicamente illustrati
nella figura 1.7.
Come abbiamo visto a pagina ![]() , il potenziale
dell'elettrodo ad
, il potenziale
dell'elettrodo ad ![]() e' dato da:
e' dato da:
da cui si vede che, una volta fissata la concentrazione di ioni
![]() in soluzione, il potenziale elettrodico e' costante (questa
e' la condizione per poter usare l'elettrodo come riferimento). Il modo
piu' banale di fissare la concentrazione di ioni
in soluzione, il potenziale elettrodico e' costante (questa
e' la condizione per poter usare l'elettrodo come riferimento). Il modo
piu' banale di fissare la concentrazione di ioni ![]() e' quello di
saturare la soluzione con un sale come
e' quello di
saturare la soluzione con un sale come ![]() : in presenza di un
corpo di fondo di
: in presenza di un
corpo di fondo di ![]() indisciolto siamo certi che la soluzione e'
satura e che, pertanto, la concentrazione di ioni
indisciolto siamo certi che la soluzione e'
satura e che, pertanto, la concentrazione di ioni ![]() al suo
interno e' costante (a temperatura costante).
al suo
interno e' costante (a temperatura costante).
L'elettrodo a calomelano e' basato sulla semireazione (punto 3):
e quindi il suo potenziale e' dato da:
(![]() e' solido e
e' solido e ![]() e' un liquido puro, quindi le loro
concentrazioni sono incluse nel termine
e' un liquido puro, quindi le loro
concentrazioni sono incluse nel termine
![]() )
)
Anche in questo caso il potenziale dipende dalla sola concentrazione
di ioni ![]() , che puo' essere facilmente mantenuta costante
operando con una soluzione satura di
, che puo' essere facilmente mantenuta costante
operando con una soluzione satura di ![]() .
.
Da quanto detto dovrebbe essere evidente la praticita' di costruzione e uso di questi due elettrodi rispetto all'elettrodo standard ad idrogeno.
21. Facciamo il punto della situazione.